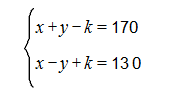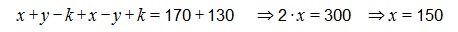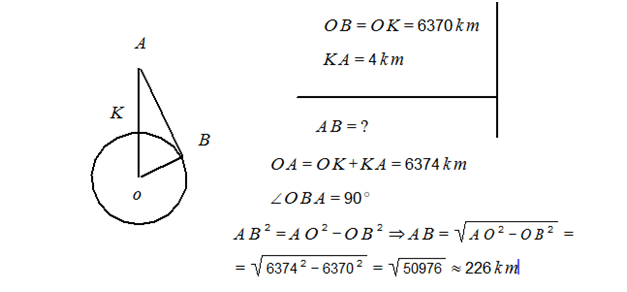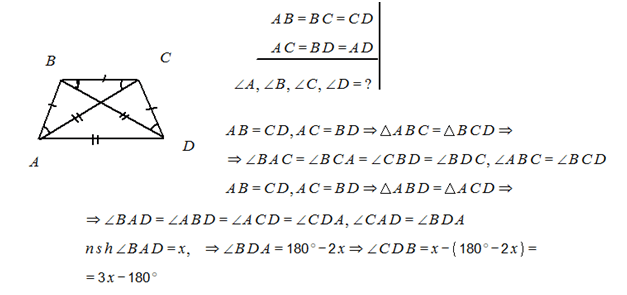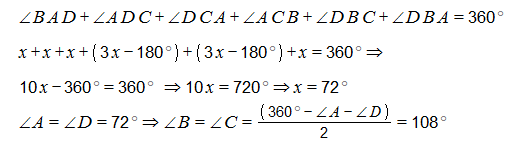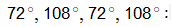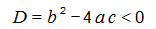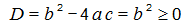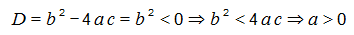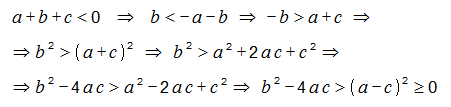Հունիս-հուլիս ամիսները ճիշտ ժամանակն է գնահատել կատարած աշխատանքները, վերլուծել բացթողումները և թերացումները:Կցանկանայի անրադառնալ մեր հեղինակային կրթության հիմնական բաղադրիչ հանդիսացող նախագծային աշխատանքների պատշաճ կատարմանը:

Պետք է շատ լրջորեն վերաբերվել նախագիծ ասվածին: Այնպես է ստացվել, որ իմ դասավանդման ժամանակահատվածը հիմնականում համնկավ կորոնավիրուսային համաճարակի ժամանակահատվածի հետ, և հիմնականում ես դասապրոցեսը իրականացնում էի հեռահար, համացանցի միջոցով: Որը շատ ավելի արդյունավետ անցավ, քան ես էի սկզբից մտածում:

Հունիս ամսին նամակագրական կապի մեջ էինք աշակերտների հետ: Քննարկում էինք ո՛չ միայն մաթեմատիկա առարկայի, այլ նաև, ֆիզիկային վերաբերվող մի շարք ահարցեր: Նախ, ի՛մ կարծիքով հնարավոր չէ, լավ ֆիզիկա իմանալ, առանց լավ մաթեմատիկա իմանալու, և հակառակը: Այս ցանկին կարելի է ավելացնել, նաև փիլիսոփայությունը:

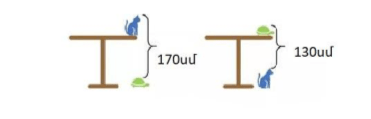
Ինչպես հունիս, այնպես էլ հուլիս ամսում, պատրաստվում ենք քննարկել ֆլեշմոբի խնդիրները, դրանց լուծման տարբերակները:

Ես ունեմ երկու կարևոր, և՛ իմ կարծիքով հետաքրքիր առաջարկներ:

1. Առաջարկում եմ, տիար Գևորգի կողմից յուրաքանչյուր ամիս ընտրել յուրաքանչյուր տարբերակից մեկական լավագույն խնդիր-վարժություն: Արդյունքում ստացվում է 5 խնդիր, իր լուծումներով: Տարվա վերջում կստացվի 60 խնդիր-վարժություն իր լուծումներով: ԵՎ կարելի է տարվա վերջում կազմել գրքույկ,

«Մխիթար Սեբաստացի» կրթահամալիր մաթեմատիկայի ֆլեշմոբի լավագույն խնդիրները և լուծումները 2020

որը կարող է դառնա կրթահամալիրի այցեքարտերից մեկը: Որը կարելի է նվիրել հյուրեր ընդունելիս, կամ հյուրընկալվելիս: Արդյունքում ավելի մեծ հետաքրքրություն կդրսևորվի դեպի մաթեմատիկան:

2. Առաջարկում եմ գույքագրել ֆիզիկայի լաբորատորիայի պարունակությունը, բոլոր հնարավոր միջոցներով համալրել այն, և շաբաթական առնվազը 1 դասաժամ հատկացնել ֆիզիկայի փորձերին: Առցանց կրթյության դեպքում կարելի է օգտվել օնլայն լաբորատորյաներից, փորձեր կատարելու համար:

Երկրորդ միջոցառման շրջանակներում արդեն պայմանավորվածություն եմ ձեռք բերել այցելել լաբորատորիա, հասկանալ ինչ կա, որքանով են սարքերը աշխատանքային վիճակում, ինչ է անհրաժեշտ համալրելու այն: Ըստ ինձ հուլիս-օգոստոս ամիսները դա իրականացնելու լավագույն ժամանակահատվածն է:

Հաշվի առնելով վերը նշվածները, հայտիս մեջ նշել եմ և՛ մաթեմատիկա և՛ ֆիզիկա առարկաները, և պատրաստ եմ մեծ պատասխանատվությամբ մոտենալ 2020-2021թթ. ուսումնական տարվա աշխատանքներին:

Մայիսյան ֆլեշմոբին արդեն մասնակցեցի և խնդիրներ կազմելով, և լուծումների իմ տարբերակը առաջարկելով: Նշեմ որ խնդիրների լուծման իմ տարբերակը առաջարկելը շատ ավելի հեշտ էր քան խնդիրների տարբերակներ առաջարկելը: Սակայն Գևորգ Հակոբյանի խորհուրդներով խնդիրների իմ առաջարկած տարբերակը ամբողջական տեսք ստացավ:

Ստորևէ ներկայացնում եմ մայիսյան ֆլեշմոբի երրորդ մակարդակի խնդիրները:

Երրորդ մակարդակ

1. Ի՞նչ ժամանակ է ցույց տալիս այս պահի դրությամբ ժամացույցը, եթե օրվա (24 ժամ) ավարտին մնացել է նրա 4/5 մասը:

2. Դրական a, b, c, d, e թվերն ընտրված են այնպես, որ ab=2, bc=3, cd=4, de=5 : Ինչի՞ է հավասար e/a հարաբերությունը :

3. ABCD քառանկյան պարագիծը 42 սմ Է: Գտեք BC կողմի երկարությունը, եթե AD=6սմ:

4. 500մ շրջանագծով շարժվում են երկու կետեր: Նրանք հանդիպում են յուրաքանչյուր 10վ հետո, եթե շարժվում են հակառակ ուղղությամբ և յուրաքանչյուր 50վ հետո, եթե շարժվում են միևնույն ուղղությամբ: Հաշվեք կետերից յուրաքանչյուրի արագությունը:

5. Քանի՞ տոկոսով կմեծանա ուղղանկյան մակերեսը, եթե նրա երկարությունը մեծացնենք 15 %-ով, իսկ լայնությունը 20 %-ով:

6. a, b, 3, 5 և 7 թվերի միջին թվաբանականը 15 է: Գտեք a և b թվերի միջին թվաբանականը:

7. Դասարանի աշակերտներից 25-ը ցանկություն հայտնեց սովորելու մաթեմատիկա, 13-ը՝ ֆիզիկա, 10-ը՝ քիմիա: Միաժամանակ մաթեմատիկա և ֆիզիկա ցանկացավ սովորել 7 աշակերտ, մաթեմատիկա և քիմիա՝ 4 աշակերտ, իսկ միաժամանակ ֆիզիկա և քիմիա ոչ մի աշակերտ չցանկացավ սովորել: Աշակերտներից յուրաքանչյուրը կարող է ընտրել երեք դասընթացից մեկը կամ երկուսը։ Քանի՞ աշակերտ է սովորում այդ դասարանում:

8. Քսանինգ թվեր՝ [-10, 14] հատվածին պատկանող բոլոր ամբողջ թվերը, տեղադրված են 5×5 չափսի աղյուսակի վանդակներում այնպես, որ յուրաքանչյուր տողում, սյունում և գլխավոր անկյունագծերում գրված թվերի գումարները նույն թիվն են ստացվել: Գտեք այդ թիվը:

9. ABC հավասարասրուն եռանկյան մեջ AB=BC: D, F և E կետերը ընտրված են այնպես, որ BD=DF=FE=EC=AC: Գտեք ABC անկյունը:

10. Աճման կարգով վերադասավորել են 1, 2, 3, 4, …, 2020, 1^2, 2^2, 3^2, 4^2, …, 2020^2 հաջորդականության անդամները: Ո՞ր թիվը կլինի նոր հաջորդականության 2020-րդ անդամը:

Խնդիրները կազմեց Թաթուլ Շահնազարյանը:

Ստորևէ ներկայացնում եմ մայիսյան ֆլեշմոբի խնդիրների լուծման իմ տարբերակը:

Մայիսյան ֆլեշմոբի լուծումները

Ապրիլյան ֆլեշմոբի խնդիրների լուծմանը առաջին անգամ մասնակցեցի: Նշեմ, որ խնդիրները շատ հետաքրքիր էին, և մեծ հաճույքով լուծեցի ինձ հատկացրած խնդիրները:

Ստորևէ ներկայացնում եմ խնդիրների լուծման իմ տարբերակը:

Ապրիլյան ֆլեշմոբի լուծումները

երկրորդ մակարդակ   8

8. Վարդուհին տետրի մեջ գրեց 11-ից մինչև 111 թվերը: Քանի՞ անգամ նա գրեց  0 թվանշանը:

Լուծում: Նախ 11-ից մինչև 100 թվերը գրելու համար հաշվենք թե քանի անգամ պետք է գրել 0 թվանշանը: Այդ թվեր են 20,30,40,…,100: Այսինքն անհրաժեշտ է  10 անգամ գրել 0 թվանշան: Այնուհետև 101-ից մինչև 111 թվերը գրելու համար հաշվենք թե քանի անգամ պետք է գրել 0 թվանշան: Այդ թվերն են 101,102,103,…,110: Այսինքն անհրաժեշտ է  10 անգամ գրել 0 թվանշան:Հետևաբար ընդամենը Վարդուհուն անհրաժեշտ կլինի 20 անգամ գրել 0 թվանշանը:

                                                                                                                  Պատ.՝ 20:

  երրորդ մակարդակ   2

2. Գտեք սեղանի բարձրությունը` օգտվելով նկարից:

Լուծում:Կատարենք հետևյալ նշանակումները:

սեղանի բարձրությունը  x,     կատվի բարձրությունը   y,

 կրյայի բարձրությունը    k: Ըստ պատկերված նկարի կունենանք՝

Համակարգի առաջի և երկրորդ հավասարումները գումարենք իրար կստանանք՝

                                                                                             Պատ.՝ 150 սմ:

 երրորդ մակարդակ    9

9. Օդապարիկը գտնվում է Երկիր մոլորակի մակերևույթից 4 կմ բարձրության վրա: Ինչքա՞ն հեռուն կարող է տեսնել օդապարիկում գտնվող մարդը, եթե հայտնի է, որ Երկրագնդի շառավիղը 6370 կմ : Պատասխանը կլորացրեք մինչև ամբողջ թիվը:

Լուծում: Խնդիրը հանգում է հետևյալ երկրաչափական խնդրին՝

Նկատենք որ AB-ն իրենից ներկայացնում է շոշափող, հետևաբար ուղղահայաց  է  OB-ին:

                                                                                Պատ.՝ 226 կմ:

   երրորդ մակարդակ   10

10. Տրված է АBCD ուռուցիկ քառանկյունը, որտեղ AB=BC=CD և անկյունագծերը հավասար են ու հավասար են АD կողմին: Հաշվեք քառանկյան անկյունները:

Լուծում:

Քանի որ քառանկյունը ուռուցիկ է հետևաբար նրա ներքին անկյունների գումարը 360 աստիճան է:

                                                                       Պատ.՝

  չորրորդ մակարդակ   10

10. Հայտնի է, որ a+b+c<0 և ax2+bx+c=0 հավասարումը իրական արմատ չունի: Որոշեք c թվի նշանը:

Լուծում: Նախ նշենք որպեսզի քառակուսային հավասարումը չունենա իրական արմատ պետք է՝ 

ա.ենթադրենք որ  c=0, այդ դեպքում կունենանք

Հետևաբար մեր հավասարումը ունի իրական արմատներ,որը հակասում է խնդրի պայմաններին, հետևաբար մեր ենթադրությունը սխալ է և :

բ.ենթադրենք   c>0  , այդ դեպքում նախ կունենանք

Եվ կատարենք հետևյալ ձևափոխությունը՝

Այս դեպքում ստանում ենք  D>0  որը հակասում է այն պայմանին,որ մեր քառակուսային հավասարումը իրական արմատներ չունի: Հետևաբար մեր ենթադրությունը սխալ է և ստանում ենք միակ հնարավոր տարբերակը՝ c<0:

                                                                                        Պատ.՝  c<0: