Ապրիլյան ֆլեշմոբ մաթեմատիկայից

Ապրիլյան ֆլեշմոբի խնդիրների լուծմանը առաջին անգամ մասնակցեցի: Նշեմ, որ խնդիրները շատ հետաքրքիր էին, և մեծ հաճույքով լուծեցի ինձ հատկացրած խնդիրները:

Ստորևէ ներկայացնում եմ խնդիրների լուծման իմ տարբերակը:

Ապրիլյան ֆլեշմոբի լուծումները

երկրորդ մակարդակ   8

8. Վարդուհին տետրի մեջ գրեց 11-ից մինչև 111 թվերը: Քանի՞ անգամ նա գրեց  0 թվանշանը:

Լուծում: Նախ 11-ից մինչև 100 թվերը գրելու համար հաշվենք թե քանի անգամ պետք է գրել 0 թվանշանը: Այդ թվեր են 20,30,40,…,100: Այսինքն անհրաժեշտ է  10 անգամ գրել 0 թվանշան: Այնուհետև 101-ից մինչև 111 թվերը գրելու համար հաշվենք թե քանի անգամ պետք է գրել 0 թվանշան: Այդ թվերն են 101,102,103,…,110: Այսինքն անհրաժեշտ է  10 անգամ գրել 0 թվանշան:Հետևաբար ընդամենը Վարդուհուն անհրաժեշտ կլինի 20 անգամ գրել 0 թվանշանը:

                                                                                                                  Պատ.՝ 20:

  երրորդ մակարդակ   2

2. Գտեք սեղանի բարձրությունը` օգտվելով նկարից:

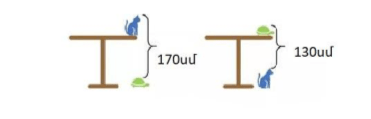
Լուծում:Կատարենք հետևյալ նշանակումները:

սեղանի բարձրությունը  x,     կատվի բարձրությունը   y,

 կրյայի բարձրությունը    k: Ըստ պատկերված նկարի կունենանք՝

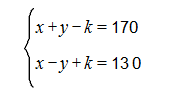
Համակարգի առաջի և երկրորդ հավասարումները գումարենք իրար կստանանք՝

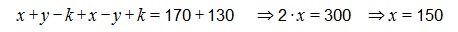
                                                                                             Պատ.՝ 150 սմ:

 երրորդ մակարդակ    9

9. Օդապարիկը գտնվում է Երկիր մոլորակի մակերևույթից 4 կմ բարձրության վրա: Ինչքա՞ն հեռուն կարող է տեսնել օդապարիկում գտնվող մարդը, եթե հայտնի է, որ Երկրագնդի շառավիղը 6370 կմ : Պատասխանը կլորացրեք մինչև ամբողջ թիվը:

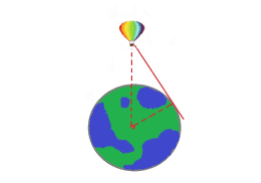
Լուծում: Խնդիրը հանգում է հետևյալ երկրաչափական խնդրին՝

Նկատենք որ AB-ն իրենից ներկայացնում է շոշափող, հետևաբար ուղղահայաց  է  OB-ին:

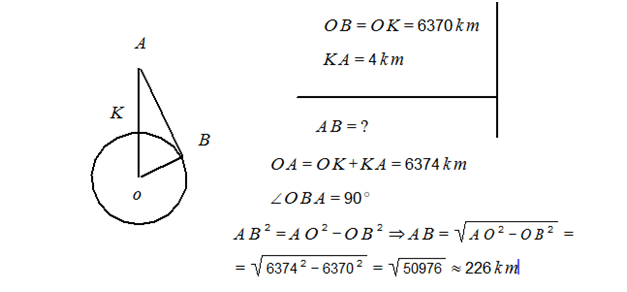
                                                                                Պատ.՝ 226 կմ:

   երրորդ մակարդակ   10

10. Տրված է АBCD ուռուցիկ քառանկյունը, որտեղ AB=BC=CD և անկյունագծերը հավասար են ու հավասար են АD կողմին: Հաշվեք քառանկյան անկյունները:

Լուծում:

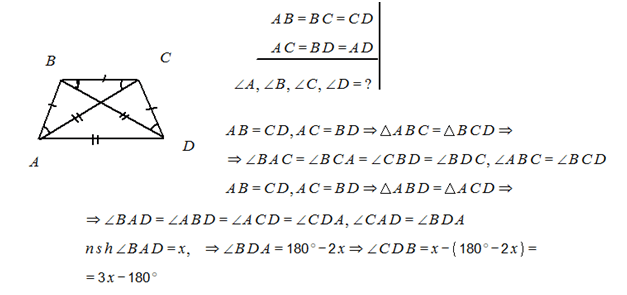
Քանի որ քառանկյունը ուռուցիկ է հետևաբար նրա ներքին անկյունների գումարը 360 աստիճան է:

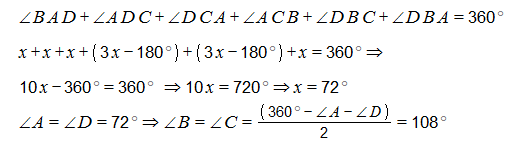
                                                                       Պատ.՝

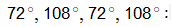
  չորրորդ մակարդակ   10

10. Հայտնի է, որ a+b+c<0 և ax2+bx+c=0 հավասարումը իրական արմատ չունի: Որոշեք c թվի նշանը:

Լուծում: Նախ նշենք որպեսզի քառակուսային հավասարումը չունենա իրական արմատ պետք է՝ 

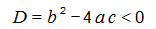
ա.ենթադրենք որ  c=0, այդ դեպքում կունենանք

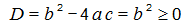
Հետևաբար մեր հավասարումը ունի իրական արմատներ,որը հակասում է խնդրի պայմաններին, հետևաբար մեր ենթադրությունը սխալ է և :

բ.ենթադրենք   c>0  , այդ դեպքում նախ կունենանք

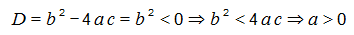
Եվ կատարենք հետևյալ ձևափոխությունը՝

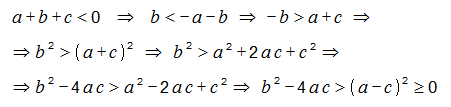
Այս դեպքում ստանում ենք  D>0  որը հակասում է այն պայմանին,որ մեր քառակուսային հավասարումը իրական արմատներ չունի: Հետևաբար մեր ենթադրությունը սխալ է և ստանում ենք միակ հնարավոր տարբերակը՝ c<0:

                                                                                        Պատ.՝  c<0: