Նախագծի ժամանակ կքննարկենք, թե՞ որոնք են կոչվում պարզ թվեր, և ինչ կիրառություն ունեն: Յուրաքանչյուր սովորող կհավաքի, պարզ թվերին վերաբերվող ցանկացած ինֆորմացիա: Կպարզենք, թե ինչպիսի՞ կիրառություն ունեն պարզ թվերը, հատկապես գաղտնագրման և կոդավորման ոլորտում :
Նախագծի նպատակը
- Սովորողների մոտ առաջացնել սեր դեպի մաթեմատիկա
- տեղեկանալ ժամանակակից մաթեմատիկայի ձեռքբերումների մասին
- կատարել հետազոտական և թարգմանչական աշխատանքներ
Նախագծի արդյունք
- Սովորողները իրենց բլոգներում հրապարակում են ստացած արդյունքները
- Իրենց բլոգներում հատուկ տեղ են հատկացնում, պարզ թվերի վերաբերյալ կատարված թարգմանություններին
- Նախագծի ավարտից հետո արդյունքները քննարկում ենք դասարանում
Ժամկետը՝ հունվարի 10-30
Մասնակիցները՝
Հիմնական նյութը՝
Մեկից մեծ բնական թիվը կոչվում է պարզ, եթե նա, չհաշված արտադրիչների հաջորդականությունը, միարժեքորեն է վերլուծվում բնական
թվերի արտադրյալի։ Հակառակ դեպքում՝ բնական թիվը կոչվում է բաղադրյալ։ Ընդգծենք, որ 1-ը չի համարվում ոչ պարզ, ոչ բաղադրյալ թիվ։ Առաջին քսան բնական թվերի հատվածում պարզ են P1= 2, P2= 3, P3= 5, P4= 7, P5= 11, P6= 13, P7= 17, P8= 19 թվերը, մնացածը, բացի 1-ից, բաղադրյալ են։ Պարզ թվերը նման են անտրոհելի տարրերի, որոնցից
բազմապատկման գործողության միջոցով կարելի է ստանալ բոլոր բնական թվերը։ Դա նման է տարրական մասնիկների դերին ֆիզիկայում կամ նրան, որ բոլոր քիմիական նյութերը կարելի է սինթեզել Մենդելեևի քիմիական տարրերի պարբերական աղյուսակի տարրերից։ Պարզ թվերի նման դերակատարումն այնքան է կարևորվել, որ համապատասխան պնդումը, ավելի ճիշտ՝ բնական թվերի՝ պարզ թվերի արտադրյալի տեսքով ներկայացման հնարավորության (այսինքն՝ գոյության) և միակության մասին պնդումը, ստացել է «թվաբանության հիմնական թեորեմ» անվանումը։
Մաթեմատիկայում և այլուր պարզ թվերը հանդիպում են ամենատարբեր իրադրություններում։ Գիտակների համար հիշատակենք, որ պարզ թվերի հետ են առնչվում, օրինակ, դաշտերի բնութագրիչները, ոչ արքիմեդյան նորմավորումները, SpecZ֊ի կետերը և այլն։
Ինչպես նշել է թվերի տեսության հայտնի մասնագետ Ա. Խինչինը. «Պարզ թվերի հիմնարար դերը մշտապես բևեռել է նրանց վրա հետազոտողների ուշադրությունը։ Ինչպիսին է նրանց բազմությունը, քա նի թիվ է պարունակում, ինչպես են նրանք
բաշխված, ինչպիսի օրինաչափությունների է ենթարկվում պարզ և բաղադրյալ թվերի իրար հաջորդումը բնական թվերի շարքում։ Բոլոր այս հարցերը բնականորեն կանգնել են տարբեր դարաշրջանների գիտնականների առջև՝ սկսած անտիկ աշխարհից
մինչև մեր օրերը, և դեռ այժմ էլ զգալի չափով գտնվում են թվաբանական գիտության ուշադրության կենտրոնում, հատկապես այն պատճառով, որ նրանց լուծումն առնչվում է արտակարգ մեծ դժվարությունների հետ»։
Գոյություն ունի հին հույներից ավանդված մի պարզ և գեղեցիկ եղանակ՝ հաջորդաբար, առանց բաց թողնելու, բոլոր պարզ թվերը ստանալու համար, որը կոչվում է էրա տ ոսթենեսի մաղ՝ այն առաջինը կիրառած հին հույն մաթեմատիկոս էրատոսթենեսի
պատվին։
Տանք հակիրճ տեղեկություններ նրա մասին։ Համարվում է, որ էրատոսթենեսը ապրել է մեր թվարկությունից առաջ 276 — 194 թթ.։ Ծնվել է Հյուսիսային Աֆրիկայի Կիրենա քաղաքում, որը գտնվում է ժամանակակից Լիբիայում, սովորել և կյանքի մեծ մասն անցկացրել է Եգիպտոսի Ալեքսանդրիա քաղաքում, նրա հռչակավոր գրադարանում։
էրատոսթենեսի բազմակողմանի գիտելիքները բարձր է գնահատել նրա ժամանակակից և
ավագ գործընկեր Արքիմեդը։
էրատոսթենեսի մաղի մեթոդը կիրառվում է հետևյալ կերպ։ Գրենք աճման կարգով բոլոր
բնական թվերը՝ սկսած երկուսից մինչև որևիցե ո բնական թիվ։ Ապա «մաղենք» այդ թվերը։ Նախ ջնջենք (կամ ընդգծենք, կամ ներկենք այլ գույնի) բոլոր այն թվերը, որոնք բաժանվում
են երկուսի՝ բացի հենց երկուսից. երկուսից հետո հաջորդ թիվը կլինի երեքը։ Թողնելով այն՝ ջնջենք բոլոր երեքի բաժանվող թվերը։ Եվ այդպես վարվենք շարոնակ, հերթական ջնջումից հետո առաջին չջնջված թիվը թողնենք, իսկ նրան բաժանվող բոլոր մնացած թվերը ջնջենք։ Գրված թվերն այսպես «մաղելուց» հետո կմնան միայն պարզ բնական թվերը, իսկ
բոլոր բաղադրյալ թվերը «կմաղվեն»։ Օրինակ՝ ո = 100 դեպքում կունենանք հետևյալ պատկերը.
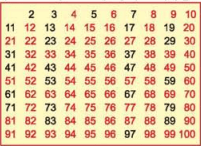
Համաձայն այս աղյուսակի՝
P15= 47, P25 = 97։ Մեծացնելով ո-ը՝ կարելի է գտնել նոր մեծամեծ պարզ թվեր։ Օրինակ՝
P35 = 149, P46= 199, P70 = 349, P95 = 499, P100 = 541, P200 = 1223, P303 = 1999։
(Այսպիսով՝ անցյալ դարի վերջին տարեթիվը պարզ էր։ Քանի պարզ տարեթիվ կլինի երրորդ
հազարամյակի առաջին դարում)
Մինչև 1950 թ. հայտնի ամե նամեծ պարզ թիվը եղել է 2127 -1 թիվը, որն ունի 39 տասնորդական թվանշան, ընդ որում, այդ թվի պարզ լինելը դեռ 1876 թ. ապացուցել է ֆրանսիացի մաթեմատիկոս Լյուկան։ 1909 թ. հրատարակվել են 10 միլիոնից փոքր բոլոր պարզ թվերի աղյուսակները։ 1951 թ. այդ աղյուսակները լրացվել են < 10999997 պարզ թվերով, իսկ 1959 թ. կազմվել է P6000000 = 104395301 պարզ թիվը չգերազանցող բոլոր պարզ թվերը պարունակող միկրոֆիլմ։ 1963 թ. հայտնի ամենամեծ պարզ թիվը 24423 -1 էր, որն ունի 1332 թվանշան։ 1985 թ. պարզ թվերի և երկվորյակ պարզ թվերի (տես ստորև) աղյուսակները հասցվել են մինչև 1011։ Հայտնի են երեք հատ 100 տասնորդական նիշ ունեցող պարզ թվեր՝ 81 * 2324 + 1, 63 * 2326+ 1, 35 * 2327 + 1 :
Ապացուցված է, որ գոյություն ունեն առնվազն երեք պարզ թվեր, որոնց թվանշանների քանակը հավասար է 1000, սակայն ոչ մի այդպիսի թիվ հայտնի չի եղել գոնե մինչև 1963 թ.։
Ցանկացած նոր պարզ թվի հայտնաբերումը համարվում է մեծ առաջընթաց։ Համակարգիչների ստեղծումից հետո սկսվում է ռեկորդների մրցավազք՝ նոր
մեծ պարզ թվեր գտնելու համար։ Եթե մինչև 1951 թ., ինչպես վերը
ասացինք, ամենամեծ հայտնի պարզ թիվը 39 նիշ ունեցող 2127–1
թիվն էր, ապա դրանից հետո տեղի է ունենում իսկական պոռթկում։ 1951 թ. մինչև 1971 թ. հայտնաբերվում են 15 նոր պարզ թվեր։ Թե նրանց հայտնաբերումն ինչ հետաքրքրություն է առաջացնում հասարակության շրջանում, վկայում է, օրինակ, հերթական նորահայտ պարզ թվին նվիրված ամերիկյան փոստային շտամպը (կնիքը), որի վրա տպված էր
«211213 — 1 » (211213 -1 թիվը պարզ է) արձանագրությունը և այդ 3 376 տասնորդական նիշ
ունեցող թիվը։ Երբ 1978 թ. երկու դպրոցական Կալիֆոռնիայից սահմանում
են նոր ռեկորդ՝ մատնանշելով 221701 -1 պարզ թիվը, մի գերմանական թերթ գրում է. «էրատոս թենեսի մաղով հաջողվել է որսալ ամենամեծ պարզ թիվը»։ Այս առիթով մասնագետներից մեկը հումորով նկատում է, որ էրատոսթենեսի մաղը դրա համար
պիտանի է նույնքան, որքան կացինը՝ ատոմի միջուկը ճեղքելու համար։
Շատ չանցած վերոհիշյալ արդյունքը գերազանցվում է, նախ ապացուցվում է, որ պարզ
են 223209 –1, ապա 244497 -1 թվերը։ 1983 թ. հայտարարվում է, որ պարզ է 25 962 թվանշանից կազմված 286243 -1 թիվը։ Թե ինչ արագությամբ են տեղի ունենում փոփոխությունները, վկայում է հետևյալը։ Ամերիկյան մաթեմատիկական ընկերության
հեղինակավոր «Nottices of the AMS» ամսագրի 2004 թ. ապրիլյան համարում «The Great Prime Number Record Races» («Մեծ պարզ թվի ռեկորդ է գրանցվել»)
հոդվածում որպես նորահայտ մեծագույն պարզ թիվ՝ նշվում է
6 320 430 տասնորդական թվանշան ունեցող 220996011 -1 թիվը, իսկ նույն ընկերության հուլիսի կեսերի Website֊ում (կայքում) տեսնում ենք, որ ամենամեծն արդեն
224036583 — 1 պարզ թիվն է, որն ունի ավելի քան յոթ միլիոն տասնորդական թվանշան։ Նշվում է նաև, որ 100 000 դոլար մրցանակ է սահմանվել 10 միլիոն թվանշանից
կազմված պարզ թվի հայտնաբերողին ։
Ստորև բերվող աղյուսակում գրանցված են առ 2008 թվականի սեպտեմբեր ամիսը հայտնի
ամենամեծ պարզ թվերը։ Առաջին սյունում համարակալվում է նրանց հաջորդականությունը նվազման կարգով, երկրորդում նշված են այդ թվերը, երրորդում՝
նրանց տասնորդական թվանշանների քանակը, չորրորդում՝ նրանց հայտնաբերման տարեթիվը։

Սույն հոդվածը տպագրության հանձնելուց հետո Ամերիկյան մաթեմատիկակ ան Միության 2008 թ. հոկտ եմբեր ամսիկայքում հայտարարություն եղավ, որ հայտնաբերվել են 13 միլիոն թվանշան ունեցող Մերսենի 45֊րդ՝ 243112609 — 1 պարզ թիվը և ապա 11 միլիոն թվանշանից կազմված Մերսենի 46-րդ՝ 237156667 -1 պարզ թիվը։ Հայտնաբերողներից
յուրաքանչյուրը ստացել է 50 հազար դոլար մրցանակ ։ Նոր՝ 150 հազար դոլար, մրցանակ
է հայտարավել 100 միլիոն կամ ավելինիշ ո ւնեցող առաջինպարզ թիվը հայտնաբերողին։
Ինչպես տեսնում ենք, 150 000 դոլար մրցանակը դեռ սպասում է իր տիրոջը։
Սովորաբար X թվից փոքր կամ հավասար պարզ թվերի քանակը նշանակում են P(X))–ով։ Ինչպես երևում է էրատոսթենեսի մաղով ստացված հարյուրից փոքր պարզ թվերի աղյուսակից, P(20) = 8, P(50) = 15, P(100) = 25։ Նմանապես (կամ օգտ վելով համապատա սխան հայտնի աղյուսակներից) կարելի է եզրակացնել, որ P(200) = 46, P(500) = 95, P(1000) = 168, P(2000) = 303։
Բերված փաստերից երևում է, որ ո բնական թվի աճին զուգընթաց պարզ թվերի խտությունը 1-ից մինչև այդ թիվն ընկած հատվածում նվազում է։ Նրանց բաշխումը գնալով նոսրանում է։ էրատոսթենեսի մաղը գնալով թվերի ավելի մեծ մասն է «բաց թողնում»։ Եթե առաջին 100 թվերից 25 են պարզ, ապա տասը միլիոնին նախորդող հարյուրյակում կա 9 պարզ թիվ, իսկ հաջորդ հարյուր թվերի հատվածում՝ ընդամենը երկու։
Կամայական ո բնական թվի համար կան պարբերաբար կրկնվող ո երկարության բնական
թվերի հաջորդականություններ, որոնցից ոչ մեկը պ ա րզ չէ։ Օրինակ՝ այդպիսին է (N + 2)–ից մինչև N + ո + 1 բնական թվերի հատվածը, որտեղ Tn = (ո + 1)! = 1*2*3*…* ո*(ո + 1)։
Կասկած է առաջանում. գուցե պարզ թվերի քանակը ընդհանրապես վերջավոր է։ Սակայն այդ վարկածն առանց դժվարության հերքվում է հակասող ենթադրությամբ։
Ենթադրենք, որ պ ա րզ թվերի հաջորդականությունը վերջավոր է, և Pn–ը ամենամեծ պարզ թիվն է։ Դիտարկենք Tn = p1 * p2 * …* pn+1 բնական թիվը և նրա բոլոր
d > 1 բաժանարարները, այսինքն՝ այնպիսի բնական թվերը, որոնց արտադրյալը որևէ բնական թվի հետ տալիս է Tn։ Ակնհայտ է, որ այդպիսի ամենափոքր բաժանարարը կլինի պարզ թիվ։ Նույնքան ակնհայտ է, որ այն չի կարող լինել p1 , p2 , …, pn թվերից որևէ մեկը (հակառակ դեպքում, 1 բնական թիվը կհանդիսանա երկու բնական թվերի արտադրյալ,
որոնցից յուրաքանչյուրը մեծ է մեկից, իսկ դա հնարավոր չէ)։ Այսպիսով՝ ստացանք, որ գոյություն ունի Pn -ից մեծ պարզ թիվ։ Դա հակասում է մեր ենթադրությանը, և ուրեմն պարզ թվերի հաջորդականությունն անվերջ է։
Առաջին անգամ այս ապացույցը բերվում է Էվկլիդեսի «Մաթեմատիկայի հիմունքներ»
տրակտատում։ Սակայն Էվկլիդեսին խորթ է անվերջության գաղափարը, և ապացուցված
փաստը նա ձևակերպում է այսպես.
«Պարզ թվերն ավելի շատ են, քան նրանց կամայական քանակը»։
Համաձայն վերը բերված ապացույցի՝ pn+ 1-ից. Tn բնական թվերի հատվածում կա գոնե
մեկ պարզ թիվ։ Դեռ 1850 թ. Չեբիշևն ուժեղացրել է այս արդյունքը՝ ապացուցելով այսպես
կոչված «Բերտրանի պոստուլատը». կամայական ո > 3 բնական թվի համար ո և 2n — 2 թվերի միջև կա առնվազն մեկ պարզ թիվ։ Կարելի է ապացուցել ավելի ուժեղ պնդում. ցանկացած ո > 5 և 2ո բնական թվերի միջև կա առնվազն երկու պարզ թիվ։
Բնական թվերի հաջորդականությունը 1 առաջին անդամով և 1 տարբերությամբ թվաբանական պրոգրեսիա է։ Կարելի է ցանկացած a և b բնական թվերի համար դնել այսպիսի ընդհանուր խնդիր. անվերջ է արդյոք պարզ թվերի քանակը b առաջինա նդամով և a տարբերությամբ թվաբանական պրոգրեսիայում։ Ակնհայտ է, որ պատասխանը
բացասական է այն դեպքում, երբ a-ն և b-ն ունեն մեկից մեծ ընդհանուր բաժանարար։ Հակառակ դեպքում, այսինքն՝ երբ a-ն ու b-ն փոխադարձաբար պարզ են, ինչպես ապացուցել է գերմանացի մաթեմատիկոս Դիրիխլեն, վերը դրված հարցի պատասխանը
դրական է. գոյություն ունեն բազմաթիվ aո + b տիպի պարզ թվեր, որտեղ ո-ը բնական թիվ է։ Սակայն խնդրի արդեն հաջորդ աստիճանի բարդացումը՝ անվերջ են արդյոք an2+bո+c
տիպի պարզ թվերը, կարծես թե, լուծված չէ անգամ պարզագույն՝ a = c = 1, b = 0 դեպքում։
Հետաքրքրական է, որ, օրինակ,
ո2 + 79ո + 1601 արտահայտությունը պարզ թվեր է տալիս ո-ի 1-ից մինչև 79՝ ներառյալ բնական արժեքների համար, սակայն ո = 80 դեպքում ստացվում է բաղադրյալ թիվ:
Հոլդբախի խնդրի մասին։ Քյոնիգսբերգ (այժմ՝ Կալինինգրադ) քաղաքում 1690 թ. ծնված
և հասուն կյանքի մեծ մասը Ռուսաստանում անցկացրած մաթեմատիկոս Քրիստիան Հոլդբախը գիտության պատմության մեջ մնացել է հիմնականում 1742թ. հռչակավոր մաթեմատիկոս էյլերին առաջարկած հետևյալ խնդրով. ճիշտ է արդյոք, որ երկուսից մեծ ցանկացած զույգ թիվ երկու պարզ թվերի գումար է (օրինակ՝ 4 = 2+2, 6 = 3+3,
8 = 3+5, 10 = 3+7 = 5+5, … ), իսկ հինգից մեծ կամայական կենտ թիվ՝ երեք պարզ թվերի գումար (7 = 2+2+3, 11 = 3+3+5, … ):
Դժվար չէ նկատել, որ այս երկու հարցադրումները համարժեք են, այսինքն՝ նրանցից մեկի ճիշտ լինելուց կհետևի մյուսի ճիշտ լինելը։ էյլերին չի հաջողվել լուծել այդ խնդիրը։ Նրա ամբողջական լուծումը չկա ցայսօր։ Առավելագույն առաջընթացը արձանագրել են ռուսական մաթեմատիկոսներ Շնիրելմանը 1930 թ. և Վինոգրադովը 1936 թ.։
Նկատենք, որ բոլոր պարզ թվերը կենտ են՝ բացի 2-ից (հին հույները հաճախ 2-ը անգամ չեն
համարել պ արզ թիվ)։ Այսինքն՝ չհաշված 2-ը և 3-ը՝ պարզ թվերի միջև կա առնվազն մեկ բաղադրյալ թիվ։ Կենտ թվերի շարքում իրար անմիջականորեն հաջորդող
երկու պարզ թվերը կոչվում են երկվորյա կ պ ա րզ թվեր։
Ւնչպես երևում է վերը բերված աղյուսակից, առաջին 100 բնական թվերի շարքում երկվորյակ պարզ թվերը հետևյալներն են. (3, 5), (5, 7), (11, 13), (17,19), (29, 31), (41, 43), (59, 61),(71, 73)։
Երեսուն միլիոնից փոքր բնական թվերի շարքում կա 152 892 այդպիսի զույգ։ 1985 թ. հայտնի ամենամեծ երկվորյակ պարզ թվերից յուրաքանչյուրն ունի 303 թվանշան։ Մինչև 2008 թ. սեպտեմբեր հայտնի ամենամեծ երկվորյակ պարզ թվերը հետևյալներն են.
Այս աղյսակի սյուները կազմված են նա խորդ աղյուսակի սկզբունքով։

Ցայսօր հայտնի չէ՝ անվերջ է արդյոք երկվորյակ պարզ թվերի քանակը։ Կան և այլ, ավելի նուրբ չլուծված խնդիրներ՝ կապված երկվորյակ պարզ թվերի հետ։ Չորս հաջորդական պարզ թվեր՝ pn , pn+1 ,pn+2 , pn+3 կարող են կազմել երկվորյակ թվերի երկու զույգ։ Օրինակ՝ ո = 3 դեպքում 5, 7, 11, 13 հաջորդական պարզ թվերից ստացվում են (5, 7) և (11, 13) երկվորյակները, իսկ ո = 5 դեպքում՝ (11, 13) և (17, 19) երկվորյակների զույգերը։ Բերված երկու դեպքերում էլ՝ pn+1 = pn+2 — 4։

Այսպիսի չորս հաջորդական պարզ թվերը կոչվում են քառյակ։ Ընթերցողին առաջարկում
ենք փորձել ինքնուրույն գտնել նոր քառյակներ։ Հաջողվել է հաշվել, որ առաջին տասը միլիոն բնական թվերի շարքում կա 899 քառյակ, իսկ տասնհինգ միլիոնում՝ 1209։ Ամենամեծ հայտնի քառյակը 1963 թ. եղել է հետևյալը. 2 863 308 731, 2 863 308
733, 2 863 308 737, 2 863 308 739։
Չապացուցված (և չհերքված) վարկած կա, որ քառյակների քանակն անվերջ է։
Երկվորյակ պարզ թվերի մասին խնդիրը կարելի է վերաձևակերպել այսպես. ճիշտ
է, որ 2-ը կարելի է անվերջ թվով եղանակներով ներկայացնել որպես երկու պարզ թվերի տարբերություն։ Կա ենթադրություն, որ կամայական զույգ թիվ կարելի է անվերջ քանակով
(եղանակներով) պատկերել որպես երկու հաջորդական պարզ թվերի՝ pn+1 — pn տարբերություն։ Սակայն ապացուցված չէ անգամ, որ յուրաքանչյուր զույգ թվի համար կա գեթ մեկ այդպիսի ներկայացում, չնայած որ դա ստուգված է շատ դեպքերի համար (4=11 -1 = 17 — 13, 6 = 29 — 23, 8 = 97 — 89 և այլն)։ Անգամ ապացուցված չէ, որ ցանկացած զույգ թիվ որևիցե (պարտադիր չէ հաջորդական) երկու պարզ թվերի տարբերություն է։
Այժմ սահմանափակվենք այսքանով։ Պարզ թվերին նվիրված երկրորդ հոդվածում մենք կանդրադառնանք նրանց մի շարք հետաքրքրաշարժ հատկություններին և հակիրճ կլուսաբանենք 2002 թ. երիտասարդ հնդիկ մաթեմատիկոսների փայլուն արդյունքը՝ պարզ թվերի վերաբերյալ, ինչպես նաև կծանոթանանք պարզ թվերի հետ սերտորեն կապված
կատարյալ, բարեկամական և շփվող թվերի հետ։

