( x1 , x2 , … , xn ) հաջորդականությունը կոչվում է ամբողջ-արժեք, եթե
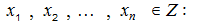
Մեկ, կամ մի քանի անհայտներից (փոփոխականներից) կախված հավասարման (հավասարումների համակարգի ) ամբողջ-արժեք լուծումը կոչվում է Դիոֆանտյան լուծում: Հավասարման (հավասարումների համակարգի ) բոլոր Դիոֆանտյան լուծումները գտնելու խնդիրը կոչվում է Դիոֆանտյան խնդիր, իսկ եթե լուծվող հավասարման (հավասարումների համակարգի ) մեջ մասնակցող բոլոր հաստատունները ամբողջ թվեր են, ապա այդ դեպքում այն կոչվում է Դիոֆանտյան հավասարում (համակարգ ): Լուծել Դիոֆանտյան հավասարումը, (համակարգը ) նշանակում է որոշել նրա լուծելիության պայմանները, և գտնել նրա բոլոր Դիոֆանտյան լուծումները:
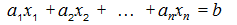
հավասարումը, որտեղ՝
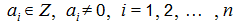
կոչվում է գծային Դիոֆանտյան հավասարում: Հակառակ դեպքում , Դիոֆանտյան հավասարումը կոչվում է ոչ գծային: Օրինակ՝
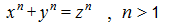
հավասարումը, ոչ գծային Դիոֆանտյան հավասարում է:
Մինչև 1994թ. թվերի տեսության ամենահայտնի չլուծված խնդիրը վերաբերվում էր հենց այս Դիոֆանտյան հավասարման լուծման գոյությանը, որը ձևակերպվել է 1637թ. ֆրանսիացի հայտնի մաթեմատիկոս ( և իրավաբան ) Պիեռ դը Ֆերմայի ( Pierre de Fermat, 1601-1665 ) կողմից ՝ հետևյալ կերպ.

Ֆերմայի մեծ (կամ վերջին ) թեորեմը: Ապացուցել, որ
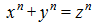
հավասարումը n > 2 դեպքում չունի (x, y, z) Դիոֆանտյան լուծումներ
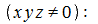
Պնդումը, ի վերջո դարձավ մաթեմատիկայի առավել նշանավոր չլուծված խնդիրներից։ Ֆերմայի վերջին թեորեմը ապացուցելու փորձերը հուշում էին, որ թվերի տեսությունը զգալիորեն զարգանում է։ Եվ ժամանակի ընթացքում Ֆերմայի վերջին թեորեմը դուրս եկավ մաթեմատիկայում չլուծված խնդիրների ցանկից։ Այն հիմնված էր Պյութագորասի թեորեմը վրա, որտեղ նշվում է, որ a2 + b2 = c2, որտեղ՝ a-ն և b-ն էջերի երկարություններն են, իսկ c-ն ներքնաձիգի։
Պյութագորասի հավասարումը, որպես լուծում ունի անվերջ թվով դրական ամբողջ թվեր՝ a, b և c։ Այս լուծումները հայտնի են որպես Պյութագորասի եռյակներ։ Ֆերման պնդեց, որ ավելի ընդհանուր հավասարումը՝ an + bn = cn չունի դրական թվերի տեսքով լուծումներ, եթե n թիվը մեծ է 2-ից։ Չնայած նրան, որ հայտարարել էր, որ ուներ ընդհանուր ապացույց իր ենթադրությունների հիման վրա, Ֆերման չթողեց իր ապացույցի մանրամասները։ Նա միայն թողեց այն հատուկ դեպքի՝ n = 4-ի ապացույցները։
Քանի որ հատուկ դեպքը՝ n = 4-ը ապացուցված էր, մնացել էր ապացուցել այն դեպքը, երբ n-ը պարզ թիվ է։ Հաջորդ երկու դարերի ընթացքում (1637–1839) վարկածը ապացուցվեց միայն 3, 5 և 7 պարզ թվերի համար։
Իսկ եթե ունենք հավասարում, որտեղ դրանցից ոչ մեկը հավասար չէ զրոյի, ուրեմն այդ հավասարումը ունի լուծում։ Որպեսզի համեմատություն կատարենք, սկսում ենք նախնական բանաձևից։

Այս թեորեմի վերջնական ապացուցումը ստացվել է 1994թ. Էնդրյու Ուալսի կողմից (Andrew Wiles ) և համարվում է XX դարում մաթեմատիկական գիտության աամենամեծ հաջողություններից մեկը:
Վերջում հետաքրքիր է լսել հետևյալ հանճարեղ երկխոսությունը՝ ՄԱԹԵՄԱՏԻԿՈՍԸ ԵՎ ՍԱՏԱՆԱՆ ։


