





















Հուլիսի ֆլեշմոբը մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես երկրորդ մակարդակի
1. Գտե’ք այն ամենափոքր թիվը, որը երկուսի, երեքի, չորսի բաժանելիս ստացվում է 1 մնացորդ, իսկ 5-ի բաժանվում է առանց մնացորդի:
2. Շոկոլադե սալիկը, տե՛ս նկարը, բաղկացած է երկու տարբեր գույնի շոկոլադներից, որոնցից յուրաքանյուրը 12 կտոր է: Տիգրանը ուզում է կտրել 2×2 սալիկ այնպես, որում երկու գույնի շոկոլադե կտորների քանակները լինեն իրար հավասար: Քանի՞ հնարավոր տարբերակ կա:
3. Շախմատի մրցաշարին մասնակցեց 7 մարդ: Մասնակիցներից յուրաքանչյուրը մնացածների հետ խաղաց մեկական պարտիա: Ընդամենը քանի՞ պարտիա անցկացվեց:
9. Պատկերը ներկիր այնպես, որ հարևան (ընդհանուր գիծ ունեցող) ցանկացած երկու մասեր լինեն տարբեր գույն, տե՛ս նկարը: Ամենաքիչը քանի՞ գույն կարող ես օգտագործել:
խնդիրները:




Սեպտեմբեր ամիսը լիարժեք աշխատեցինք ֆիզիկական միջավայրում: Ինչպես որ նախատեսել էինք սեպտեմբերին , 6-րդ , 9-րդ, 10-րդ և 11-րդ, 12-րդ դասարանցիների հետ իրականացրեցինք նախատեսված բոլոր դասընթացները և նախագծերը:
Կարևոր եմ համարում նաև սեպտեմբեր ամսում բարձունքի հաղթահարումը, իսկ ամփոփումը. Արագածի հարավային գագաթ. Հաշվետվություն տեղադրված է իմ բլոգում:
Սեպտեմբեր ամսում մասնակցել եմ մաթեմատիկայի ֆլեշմոբի օգոստոս ամսվա խնդիրների քննարկմանը և լուծմանը:
Այս ամիս մասնակցել եմ մաթեմատիկա դասավանդողների հավաքին,որը Գևորգ Հակոբյանի հետ կայացել է սեպտեմբերի 6, 13, 27 :
Ելնելով Ուսումնական պարապմունքի կազմակերպման կարգից, սեպտեմբեր ամսում ուսումնասիրեցինք.
9-դասարան հանրահաշիվ
9-րդ դասրան երկրաչափություն
թեմաները:
10-րդ, 11-րդ , 12-րդ դասարանների հետ ընդհանուր առմամբ նույնպես աշխատեցինք լիարժեք:
6-րդ դասարանցիների հետ անցանք հետևյալ թեմաները՝









«Կենգուրու»մաթեմատիկական մրցույթին ընդառաջ, «Կենգուրու»մրցույթի խնդիրների քննարկում,փետրվար, մարտ
«Պի» թվի տոն-մարտի 14
Պի թիվ կամ 

 -ն իռացիոնալ թիվ է, այսինքն՝ նրա արժեքը հնարավոր չէ ներկայացնել m/n կոտորակի տեսքով, որտեղ m-ը և n-ը ամբողջ թվեր են։ Հետևաբար, նրա տասական ներկայացումը երբեք չի վերջանում և չի հանդիսանում պարբերական։
-ն իռացիոնալ թիվ է, այսինքն՝ նրա արժեքը հնարավոր չէ ներկայացնել m/n կոտորակի տեսքով, որտեղ m-ը և n-ը ամբողջ թվեր են։ Հետևաբար, նրա տասական ներկայացումը երբեք չի վերջանում և չի հանդիսանում պարբերական։  թվի իռացիոնալությունը առաջին անգամ ապացուցվել է Իոհան Լամբերտի կողմից 1761 թվականին
թվի իռացիոնալությունը առաջին անգամ ապացուցվել է Իոհան Լամբերտի կողմից 1761 թվականին  թվի տրոհումը անընդհատ կոտորակի։ 1794 թվականին Լեժանդրը բերեց
թվի տրոհումը անընդհատ կոտորակի։ 1794 թվականին Լեժանդրը բերեց  թվերի իռացիոնալության առավել խիստ ապացույց։
թվերի իռացիոնալության առավել խիստ ապացույց։ -ն տրանսցենդենտ թիվ է, այսինքն այն չի կարող լինել որևէ ամբողջ գործակիցներով բազմանդամի արմատ։
-ն տրանսցենդենտ թիվ է, այսինքն այն չի կարող լինել որևէ ամբողջ գործակիցներով բազմանդամի արմատ։  թվի տրանսցենդենտությունը 1882 թվականին ապացուցվել է քյոնինգսբերգյան պրոֆեսորի կողմից, իսկ հետագայում մյունխենյան համալսարանից Ֆերդինանդ ֆոն Լինդեմանի կողմից։ Ապացույցը պարզեցրեց Ֆելիքս Կլեյնը 1894 թվականին։
թվի տրանսցենդենտությունը 1882 թվականին ապացուցվել է քյոնինգսբերգյան պրոֆեսորի կողմից, իսկ հետագայում մյունխենյան համալսարանից Ֆերդինանդ ֆոն Լինդեմանի կողմից։ Ապացույցը պարզեցրեց Ֆելիքս Կլեյնը 1894 թվականին։ թվից, ապա
թվից, ապա  թվի տրանսցենդենտության ապացույցը վերջ դրեց շրջանի քառակուսացուման վեճին, որը տևեց ավելի քան 2, 5 հազար տարի։
թվի տրանսցենդենտության ապացույցը վերջ դրեց շրջանի քառակուսացուման վեճին, որը տևեց ավելի քան 2, 5 հազար տարի։ թվի տրանսցենդենտությունը։ 1996 թվականին Յուրի Նեստերենկոն ապացուցեց, որ ցանկացած բնական
թվի տրանսցենդենտությունը։ 1996 թվականին Յուրի Նեստերենկոն ապացուցեց, որ ցանկացած բնական  թվի համար
թվի համար  և
և  թվերը հանրահաշվորեն անկախ են, որից մասնավորապես հետևում է
թվերը հանրահաշվորեն անկախ են, որից մասնավորապես հետևում է  և
և  թվերի տրանսցենդենտությունը։
թվերի տրանսցենդենտությունը։ -ն հանդիսանում է պարբերությունների օղակի տարր (հետևաբար, հաշվելի և թվաբանական թիվ)։ Սակայն անհայտ է, արդյոք
-ն հանդիսանում է պարբերությունների օղակի տարր (հետևաբար, հաշվելի և թվաբանական թիվ)։ Սակայն անհայտ է, արդյոք  -ը պատկանում է պարբերությունների օղակին։
-ը պատկանում է պարբերությունների օղակին։
Ստորակետից հետո 
Առաջին անգամ հունարեն 
Այս նշանակումը առաջացել է հունարեն՝ περιφέρεια (շրջանագիծ) և περίμετρος (պարագիծ) բառերի առաջին տառից։ 









Հուլիսի ֆլեշմոբը մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես չորրորդ մակարդակի
4. Տրված է PQRS քառակուսին և PS կողմի M միջնակետը: Որքա՞ն է QMS եռանկյան և PQRS քառակուսու մակերեսների հարաբերությունը:
3. Շրջանագծի վրա նշված է 17 կետ: Նրանցից յուրաքանչյուրը միացված է մյուսների հետ, բացի իր անմիջական հարևաններից: Քանի՞ լար կստացվի:
1. 3 թվի 40 տոկոսը բազմապատկեցին 3 թվի 60 տոկոսով: Արդյունքում 3 թվի քանի՞ տոկոսը ստացվեց:
խնդիրները:
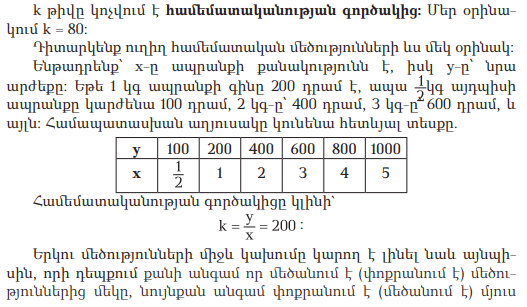
ԱՌԱՋԱԴՐԱՆՔՆԵՐԻ ՓԱԹԵԹ
«Մխիթար Սեբաստացի» կրթահամալիր
(Մխիթար Սեբաստացի) կրթահամալիր Ավագ դպրոց
<<Մխիթար Սեբաստացի>> կրթահամալիր