9-րդ դասարանցիներ
Ժամկետը՝ շուրջտարյա
Մաթեմատիկան հին Հնդկաստանում և հին Չինաստանում
Մանակիցները տեղեկություն են գտնում հին Հնդկաստանի և հին Չինաստանի մաթեմատիկոսների մասին:
Դպրոցական դասագրքերից, այլ աղբյուրներից , համացանցից , հավաքում եմ հին խնդիրներ , մասնավորապես խնդիրներ որոնք ստեղծվել են հին Հնդկաստանում և հին Չինաստանում:
Խնդիրների ժողովածուի ստեղծում։
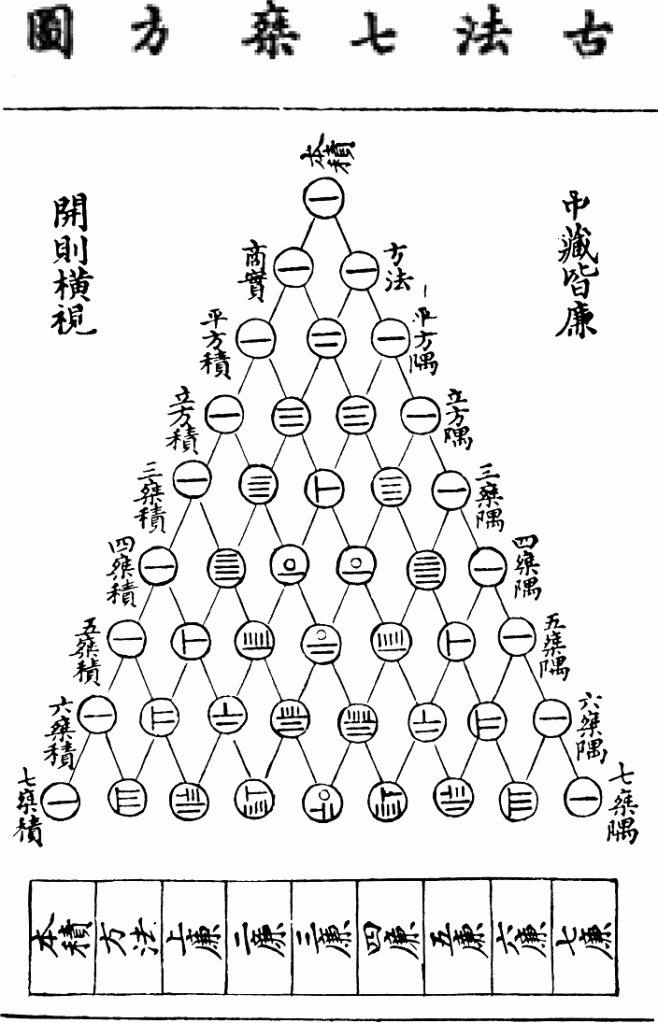
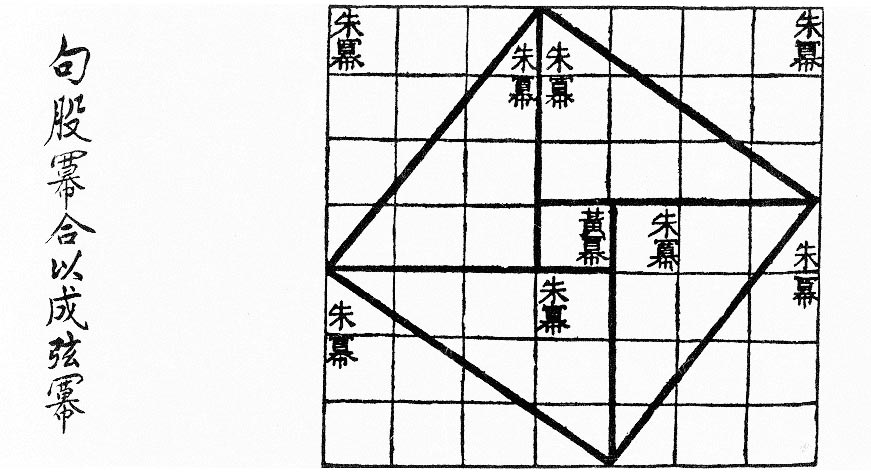
Նախագծի նպատակը՝
Միջին և ավագ դպրոցի սովորողները ծանոթանում են հին արևելքի մաթեմատիկայի և մաթեմատիկոսների հետ։
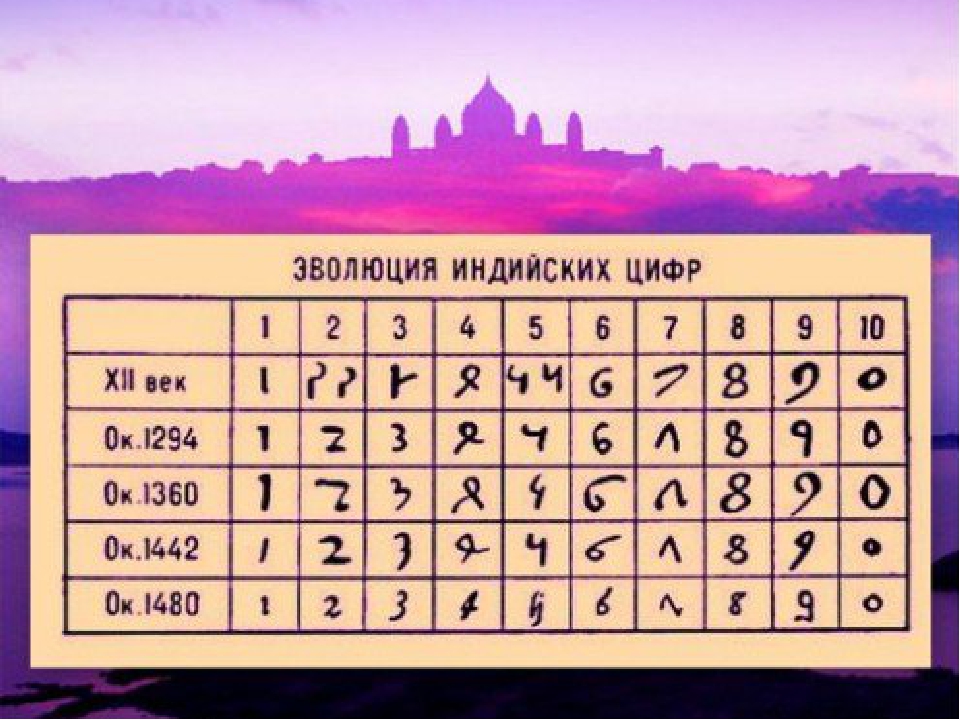
Խնդիրներ` հին չինական «Ինը գիրք մաթեմատիկայի մասին» գրքից:
- «Ջրամբարի լայնությունը 2.4 ջան է՝ (1 ջանը = 10 չի): Ջրամբարի կենտրոնում աճում է եղեգը, որը ջրի մակարդակից 6 չի բարձր է: Եղեգը կարելի է ճկել այնպես, որ նրա գագաթը հասնի ափին: Գտիր ջրամբարի խորությունը և եղեգի բարձրությունը»:

Տեղեկանք: 1 ջանը (հին չինական չափման միավոր) մոտավորապես հավասար է 3,2 մետրի:
2. Վանդակում կան անհայտ թվով միրհավներ և նապաստակներ։ Հայտնի է, որ ամբողջ վանդակում կա 35 գլուխ և 94 ոտք։ Գտնել միրհավների և նապաստակների թիվը։
3. Լավ բերքի 3 խրձից, միջին բերքի 2 խրձից և վատ բերքի 1 խրձից միասին ստացվում է 39 դոու ցորեն։ Լավ բերքի 2 խրձից, միջին բերքի 3 խրձից և վատ բերքի 1 խրձից միասին ստացվում է 34 դոու ցորեն։ Լավ բերքի 1 խրձից, միջին բերքի 2 խրձից և վատ բերքի 3 խրձից միասին ստացվում է 26 դոու ցորեն։ Որքան ցորեն կստացվի լավ բերքի 1 խրձից, միջին բերքի 1 խրձից և վատ բերքի 1 խրձից:
Սերգեյ Մերգելյան
Մերգելյանի մասին նյութեր են հրապարակել իրենց բլոգներում հետևյալ սովորողները
Որպես արդյունք սովորողները ծանոթացան հին Չինական մի քանի խնդիրների, դրանց լուծման ընթացքին, և ամենակարևոր արդյունքը կարելի է առանձնացնել այն, որ սովորողները ճանաչեցին Սերգեյ Մերգելյանին, ծանոթացան նրա գործնեությանը և կյանքի:
Եվ այդ ամենի ընդացքում ավելի ամրապնդվեց սերը դեպի մաթեմատիկա և ճշգրիտ գիտություն:
Մերգելյանի թեորեմ
Մերգելյանի թեորեմ, կոմպլեքս անալիզի հայտնի արդյունք՝ ապացուցված հայ մաթեմատիկոս Սերգեյ Մերգելյանի կողմից 1951 թվականին։ Այն պնդում է հետևյալը.
Դիցուք, K-ն C կոմպլեքս հարթության կոմպակտ ենթաբազմություն է այնպես, որ C∖K -ն կապակցված է, այսինքն՝ չենք կարող այն տրոհել երկու ոչ դատարկ ենթաբազմությունների այնպես, որ դրանցից յուրաքանչյուրը ընդհանուր կետ չունենա մյուս ենթաբազմության փակման հետ։ Այդ դեպքում՝ ցանկացած f : K →C անընդհատ ֆունկցիա, որի նեղացումը int(K)-ի վրա հոլոմորֆ է, կարելի է K-ի վրա հավասարաչափ մոտարկել բազմանդամներով։ Այստեղ int(K)-ն K ենթաբազմության ներքին տիրույթն է։
Մերգելյանի թեորեմը Վայերշտրասի մոտարկման թեորեմի և Ռունգեի թեորեմի վերջնական կատարելագործումն ու ընդհանրացումն է։ Այն տալիս է բազմանդամներով մոտարկման դասական խնդրի բարդ լուծումը։
Այն դեպքում, երբ C∖K -ն կապակցված չէ, նախնական մոտարկման խնդրում բազմանդամները պետք է փոխարինվեն ռացիոնալ ֆունկցիաներով։ Ռացիոնալ մոտարկման խնդրի լուծման կարևոր քայլը ևս առաջարկվել է Մերգելյանի կողմից 1952 թվականին։ Ռացիոնալ մոտարկման վերաբերյալ հետագա խորքային քայլերը հիմնականում արվել են Ա․ Գ․ Վիտուշկինի կողմից։
Վայերշտրասի և Ռունգեի թեորեմները առաջարկվել են 1885 թ.-ին, միչդեռ Մերգելյանի թեորեմը թվագրվում է 1951 թ.-ին։ Ժամանակային այս հսկայական տարբերությունը զարմանալի չէ, քանի որ Մերգելյանի թեորեմի ապացույցը հիմնված է հզոր մեթոդի վրա, որը ստեղծել է Մերգելյանը։ Վայերշտրասից և Ռունգեից հետո մի շարք մաթեմատիկոսներ (մասնավորապես ՈՒոլշը, Կելդիշը և Լավրենտևը) նույնպես աշխատել են նույն խնդրի վրա։ Մերգելյանի առաջարկած լուծումը կառուցողական է և մինչ օրս մնում է միակը իր տեսակի մեջ։

