11. Վերածվող հավասարումներ
Месяц: Октябрь 2022
Այցելություն Պրոֆեսոր Հ. Կարապետյանի անվան Երկրաբանական թանգարան
Վայրը՝ Պրոֆեսոր Հ. Կարապետյանի անվան
Երկրաբանական թանգարան
Ճամփորդության օրը՝ 10.11.22թ․ (12:40-15:00)
Նախապատրաստում՝
- սովորողները ծանոթանում են երկրաբանության հետ
- ծանոթանում են թանգարանի կայքին
Նպատակը
- Նախասիրությունների բացահայտում
Խնդիրներ
- Սովորողների մոտ առաջացնել հետաքրքրություն գիտության, երկրաբանության, հնէաբանության, օգտակար հանածոների նկատմամբ
- Ձևավորել մասնագիտական կողմնորոշում
Ճամփորդության ընթացքը
- շրջայց թանգարանում
- ծանոթացում ցուցադրությանը
- հարց ու պատասխան
Անհրաժեշտ իրեր
- տեսագրող և լուսանկարահանող սարքեր
Երթուղի՝ Մայր դպրոցի բակ, Ծովակալ Իսակովի պողոտա, Մաշտոցի պողոտա, Մարշալ Բաղրամյանի պողոտա
Բուժարկղիկը՝ դպրոցի բուժսենյակից
Համակարգող՝
- Թաթուլ Շահնազարյան (099527790)
Տրանսպորտ՝ 60OC077
Վարորդ՝ Սահակյան Վարդան (099339009)
Գումարը՝ մեկ անձը 1 000 դրամ
Վճարող- ծնող
Թանգարանի մուտքը՝ Ավագ դպրոցի տրամադրած աբոնեմենտներով
Ակնկալվող արդյունք՝ ճամբարականները կներկայանան պատումներով, ֆոտոշարքով, տեսանյութերով, որոնք կհրապարակվեն ճամբարականների բլոգներում, ենթակայքում, կայքում։
Մասնակիցներ՝ Ավագ դպրոցի 9-րդ դասարանի սովորողներ
- Սահակյան Անիտա
- Ղազարյան Ակսել
- Կույումջյան Արեգ
- Բարսեղյան Գոհար
- Խաչատրյան Նանե
- Գյուրջինյան Իրինա
- Հովհաննիսյան Անահիտ
- Վահանյան Ալեքս
- Մուրադյան Դավիթ
- Ղազարյան Անգելինա
- Հովհաննիսյան Մանե
- Մուշեղյան Արամ
Սեբաստացու օրեր. կրթահամալիրի տոն 2022-2023
9, 10, 11, 12-րդ դասարանցիներ
Ժամկետը՝ շուրջտարյա
Մաթեմատիկան հին Հնդկաստանում և հին Չինաստանում
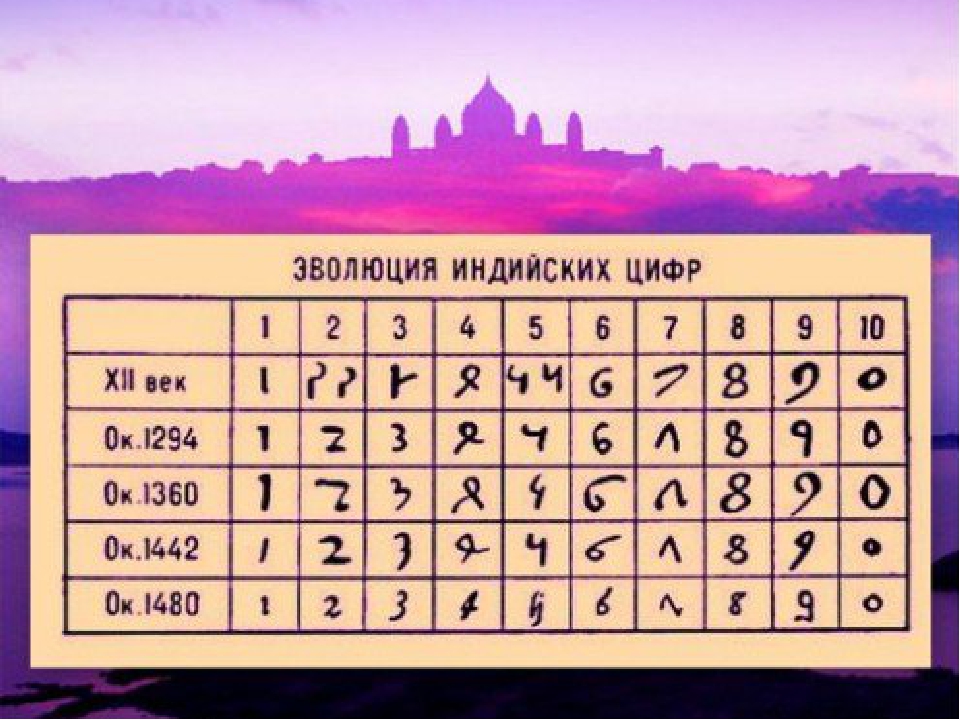
Մանակիցները տեղեկություն են գտնում հին Հնդկաստանի և հին Չինաստանի մաթեմատիկոսների մասին:
Դպրոցական դասագրքերից, այլ աղբյուրներից , համացանցից , հավաքում եմ հին խնդիրներ , մասնավորապես խնդիրներ որոնք ստեղծվել են հին Հնդկաստանում և հին Չինաստանում:
Խնդիրների ժողովածուի ստեղծում։
Նախագծի նպատակը՝
Միջին և ավագ դպրոցի սովորողները ծանոթանում են հին արևելքի մաթեմատիկայի և մաթեմատիկոսների հետ։
Խնդիրներ` հին չինական «Ինը գիրք մաթեմատիկայի մասին» գրքից:
- «Ջրամբարի լայնությունը 2.4 ջան է՝ (1 ջանը = 10 չի): Ջրամբարի կենտրոնում աճում է եղեգը, որը ջրի մակարդակից 6 չի բարձր է: Եղեգը կարելի է ճկել այնպես, որ նրա գագաթը հասնի ափին: Գտիր ջրամբարի խորությունը և եղեգի բարձրությունը»:
Տեղեկանք: 1 ջանը (հին չինական չափման միավոր) մոտավորապես հավասար է 3,2 մետրի:
2. Վանդակում կան անհայտ թվով միրհավներ և նապաստակներ։ Հայտնի է, որ ամբողջ վանդակում կա 35 գլուխ և 94 ոտք։ Գտնել միրհավների և նապաստակների թիվը։
3. Լավ բերքի 3 խրձից, միջին բերքի 2 խրձից և վատ բերքի 1 խրձից միասին ստացվում է 39 դոու ցորեն։ Լավ բերքի 2 խրձից, միջին բերքի 3 խրձից և վատ բերքի 1 խրձից միասին ստացվում է 34 դոու ցորեն։ Լավ բերքի 1 խրձից, միջին բերքի 2 խրձից և վատ բերքի 3 խրձից միասին ստացվում է 26 դոու ցորեն։ Որքան ցորեն կստացվի լավ բերքի 1 խրձից, միջին բերքի 1 խրձից և վատ բերքի 1 խրձից:
Սերգեյ Մերգելյան
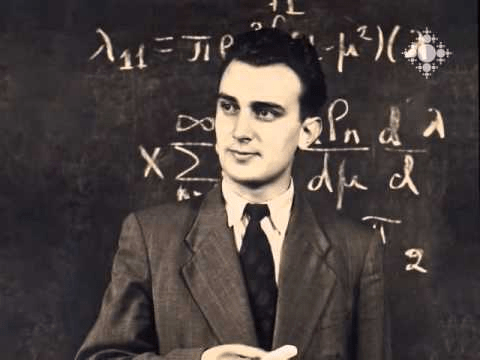
Որպես արդյունք սովորողները ծանոթացան հին Չինական մի քանի խնդիրների, դրանց լուծման ընթացքին, և ամենակարևոր արդյունքը կարելի է առանձնացնել այն, որ սովորողները ճանաչեցին Սերգեյ Մերգելյանին, ծանոթացան նրա գործնեությանը և կյանքի:
Եվ այդ ամենի ընդացքում ավելի ամրապնդվեց սերը դեպի մաթեմատիկա և ճշգրիտ գիտություն:
Մերգելյանի թեորեմ
Մերգելյանի թեորեմ, կոմպլեքս անալիզի հայտնի արդյունք՝ ապացուցված հայ մաթեմատիկոս Սերգեյ Մերգելյանի կողմից 1951 թվականին։ Այն պնդում է հետևյալը.
Դիցուք, K-ն C կոմպլեքս հարթության կոմպակտ ենթաբազմություն է այնպես, որ C∖K -ն կապակցված է, այսինքն՝ չենք կարող այն տրոհել երկու ոչ դատարկ ենթաբազմությունների այնպես, որ դրանցից յուրաքանչյուրը ընդհանուր կետ չունենա մյուս ենթաբազմության փակման հետ։ Այդ դեպքում՝ ցանկացած f : K →C անընդհատ ֆունկցիա, որի նեղացումը int(K)-ի վրա հոլոմորֆ է, կարելի է K-ի վրա հավասարաչափ մոտարկել բազմանդամներով։ Այստեղ int(K)-ն K ենթաբազմության ներքին տիրույթն է։
Մերգելյանի թեորեմը Վայերշտրասի մոտարկման թեորեմի և Ռունգեի թեորեմի վերջնական կատարելագործումն ու ընդհանրացումն է։ Այն տալիս է բազմանդամներով մոտարկման դասական խնդրի բարդ լուծումը։
Այն դեպքում, երբ C∖K -ն կապակցված չէ, նախնական մոտարկման խնդրում բազմանդամները պետք է փոխարինվեն ռացիոնալ ֆունկցիաներով։ Ռացիոնալ մոտարկման խնդրի լուծման կարևոր քայլը ևս առաջարկվել է Մերգելյանի կողմից 1952 թվականին։ Ռացիոնալ մոտարկման վերաբերյալ հետագա խորքային քայլերը հիմնականում արվել են Ա․ Գ․ Վիտուշկինի կողմից։
Վայերշտրասի և Ռունգեի թեորեմները առաջարկվել են 1885 թ.-ին, միչդեռ Մերգելյանի թեորեմը թվագրվում է 1951 թ.-ին։ Ժամանակային այս հսկայական տարբերությունը զարմանալի չէ, քանի որ Մերգելյանի թեորեմի ապացույցը հիմնված է հզոր մեթոդի վրա, որը ստեղծել է Մերգելյանը։ Վայերշտրասից և Ռունգեից հետո մի շարք մաթեմատիկոսներ (մասնավորապես ՈՒոլշը, Կելդիշը և Լավրենտևը) նույնպես աշխատել են նույն խնդրի վրա։ Մերգելյանի առաջարկած լուծումը կառուցողական է և մինչ օրս մնում է միակը իր տեսակի մեջ։
Հետևյալ սովորողները մասնակցել են վերը նշված նախագծին։
Հոկտեմբեր ամսվա աշխատանքների ամփոփում
Հոկտեմբեր ամիսը լիարժեք աշխատեցինք ֆիզիկական միջավայրում: Ինչպես որ նախատեսել էինք հոկտեմբերին 9-րդ, 10-րդ, 11-րդ և 12-րդ դասարանցիների հետ իրականացրեցինք նախատեսված բոլոր դասընթացները և նախագծերը:
Կարևոր եմ համարում որպես նախասիրությունների բացահայտում, հոկտեմբերի 13-ին կազմակերպված Այցելություն Գիտության և Տեխնիկայի Թանգարան ճամփորդությունը, որի ամփոփումը՝ Այցելություն Գիտության և Տեխնիկայի Թանգարան․ Ամփոփում տեղադրված է իմ բլոգում:
Կազմել եմ մաթեմատիկական ֆլեշմոբի հոկտեմբեր ամսվա երկրորդ մակարդակի խնդիրները:
Հոկտեմբեր ամսում մասնակցել եմ մաթեմատիկայի ֆլեշմոբի, սեպտեմբեր ամսվա խնդիրների քննարկմանը և լուծմանը:
Մասնակցել եմ նաև Աշնանային 17-րդ մանկավարժական ճամբարին:
Այս ամիս մասնակցել եմ ուսուցիչների պարտադիր ատեստավորման բոլոր փուլերին:
Կարևոր եմ համարում նշել ուսուցիչների պարտադիր ատեստավորման հետազոտական աշխատանքի ավարտը և հրապարակումը:
Ելնելով Ուսումնական պարապմունքի կազմակերպման կարգից, սեպտեմբեր ամսում ուսումնասիրեցինք.
9-դասարան հանրահաշիվ
- 7.Ռացիոնալ անհավասարումների լուծումը
- 8. Ռացիոնալ անհավասարումների համակարգեր և համախմբեր
- 9. Գաղափար ռացիոնալ հավասարման մասին
- 10.Երկքառակուսային հավասարումներ
9-րդ դասրան երկրաչափություն
թեմաները:
10-րդ, 11-րդ , 12-րդ դասարանների հետ ընդհանուր առմամբ նույնպես աշխատեցինք լիարժեք:
Այցելություն Գիտության և Տեխնիկայի Թանգարան․ Ամփոփում
Ինչպես, որ նախատեսել եինք << Այցելություն Գիտության և Տեխնիկայի Թանգարան>> ճամփորդությունը կազմակերպեցինք՝ 13.10.22թ․ (12:40-15:00)։
Ճամփորդության հիմնական նպատակն ու խնդիրները գրված է ստորև՝
Նպատակը
- Նախասիրությունների բացահայտում
Խնդիրներ
- Սովորողների մոտ առաջացնել հետաքրքրություն գիտության, տեխնիկայի և գյուտարարության հանդեպ
- Ձևավորել մասնագիտական կողմնորոշում
Ճամփորդություն առջև դրված խնդիրը համարում եմ կատարված։
Ստորև ներկայացնում եմ որոշակի սովորողների ամփոփումներ, հրապարակված իրենց բլոգներում։
Ճամփորդությունը համարում եմ լիարժեք կայացած։
Մանկավարժական ճամբար
Հոկտեմբերի 24-28
Հոկտեմբերի 24
- 09։00՝ մանկավարժական խորհրդով քննարկում․ Հեղինակային կրթական ծրագրով կամավոր ատեստավորման իր փաթեթը ներկայացնում է Վարդան Կարապետյանը
- 10։00-11։00՝
Սարալանջում՝
- Թաթուլ Շահնազարյան
- Վարդան Կարապետյան
- 12։00-ից ընդմիջում
- 13։00՝ աշխատանք մասնախմբերով
Հոկտեմբերի 25
- 09։00՝ Համընդհանուր ներառականություն․ հատուկ կարիքով սովորողների հետ աշխատանք, խնդիրներ, լուծումներ/Սուսաննա Չալիկյան/
- 10։00-12։00՝ աշխատանք բլոգում
- 12։00-ից ընդմիջում
- 13։00՝ աշխատանք մասնախմբերով
Հոկտեմբերի 26
- 09։00՝ մանկավարժական խորհրդով քննարկում․ Գնահատում
- 10։00-11։00՝ սովորողների բլոգների ստուգում: 10-11 դասարաններ
- 11:00-12:00` կլոր սեղան․ 9-րդ դասարանների նախասիրությունների բացահայտման նախագծի առաջին փուլի ներկայացում
- 12։00-ից ընդմիջում
- 13։00՝ ընդհանուր պարապմունք մարմարյա սրահում
- 15։15․ Համերգ ֆիլհարմոնիկում «Սեբաստիա» համերգասրահ
Հոկտեմբերի 27
- 09։00՝ մանկավարժական խորհրդով քննարկում․ Սեբաստացու օրեր,կրթահամալիրի տոնի նախագծերի քննարկում
- 10։00-12։00՝ սովորողների բլոգների ստուգում: 10-11 դասարաններ
- 12։00-ից ընդմիջում
- 13։00՝ աշխատանք մասնախմբերով
Հոկտեմբերի 28
- 09։00՝ Ուսումնական ժամերգություն
- 09։30՝ մանկավարժական խորհրդով քննարկում․ընտրությամբ գործունեությունների կազմակերպումը 9-րդ դասարաններում
- 10։30-12։00՝ սովորողների բլոգների ստուգում: 10-11 դասարաններ
- 12։00-ից ընդմիջում
- 13։00-ից՝ աշխատանք մասնախմբերով
- 15։00՝ Ուրբաթ-համերգ
2.ԹՎԱՅԻՆ ԱՐԳՈՒՄԵՆՏԻ ԵՌԱՆԿՅՈՒՆԱՉԱՓԱԿԱՆ ՖՈՒՆԿՑԻԱՆԵՐԸ
5. Վեկտորի բազմապատկումը թվով
10.Երկքառակուսային հավասարումներ
ՌԱԴԻԱՆ: ԴՐԱԿԱՆ և ԲԱՑԱՍԱԿԱՆ ՊՏՈՒՅՏՆԵՐ
Թաթուլ Շահնազարյան 