Рубрика: ԻՄ ՍՏԵՂԾԱԾ ՆՅՈՒԹԵՐԸ
ՖԵՐՄԱՅԻ ՄԵԾ ԹԵՈՐԵՄԸ
( x1 , x2 , … , xn ) հաջորդականությունը կոչվում է ամբողջ-արժեք, եթե
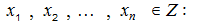
Մեկ, կամ մի քանի անհայտներից (փոփոխականներից) կախված հավասարման (հավասարումների համակարգի ) ամբողջ-արժեք լուծումը կոչվում է Դիոֆանտյան լուծում: Հավասարման (հավասարումների համակարգի ) բոլոր Դիոֆանտյան լուծումները գտնելու խնդիրը կոչվում է Դիոֆանտյան խնդիր, իսկ եթե լուծվող հավասարման (հավասարումների համակարգի ) մեջ մասնակցող բոլոր հաստատունները ամբողջ թվեր են, ապա այդ դեպքում այն կոչվում է Դիոֆանտյան հավասարում (համակարգ ): Լուծել Դիոֆանտյան հավասարումը, (համակարգը ) նշանակում է որոշել նրա լուծելիության պայմանները, և գտնել նրա բոլոր Դիոֆանտյան լուծումները:
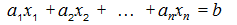
հավասարումը, որտեղ՝
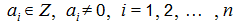
կոչվում է գծային Դիոֆանտյան հավասարում: Հակառակ դեպքում , Դիոֆանտյան հավասարումը կոչվում է ոչ գծային: Օրինակ՝
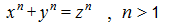
հավասարումը, ոչ գծային Դիոֆանտյան հավասարում է:
Մինչև 1994թ. թվերի տեսության ամենահայտնի չլուծված խնդիրը վերաբերվում էր հենց այս Դիոֆանտյան հավասարման լուծման գոյությանը, որը ձևակերպվել է 1637թ. ֆրանսիացի հայտնի մաթեմատիկոս ( և իրավաբան ) Պիեռ դը Ֆերմայի ( Pierre de Fermat, 1601-1665 ) կողմից ՝ հետևյալ կերպ.

Ֆերմայի մեծ (կամ վերջին ) թեորեմը: Ապացուցել, որ
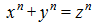
հավասարումը n > 2 դեպքում չունի (x, y, z) Դիոֆանտյան լուծումներ
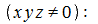
Պնդումը, ի վերջո դարձավ մաթեմատիկայի առավել նշանավոր չլուծված խնդիրներից։ Ֆերմայի վերջին թեորեմը ապացուցելու փորձերը հուշում էին, որ թվերի տեսությունը զգալիորեն զարգանում է։ Եվ ժամանակի ընթացքում Ֆերմայի վերջին թեորեմը դուրս եկավ մաթեմատիկայում չլուծված խնդիրների ցանկից։ Այն հիմնված էր Պյութագորասի թեորեմը վրա, որտեղ նշվում է, որ a2 + b2 = c2, որտեղ՝ a-ն և b-ն էջերի երկարություններն են, իսկ c-ն ներքնաձիգի։
Պյութագորասի հավասարումը, որպես լուծում ունի անվերջ թվով դրական ամբողջ թվեր՝ a, b և c։ Այս լուծումները հայտնի են որպես Պյութագորասի եռյակներ։ Ֆերման պնդեց, որ ավելի ընդհանուր հավասարումը՝ an + bn = cn չունի դրական թվերի տեսքով լուծումներ, եթե n թիվը մեծ է 2-ից։ Չնայած նրան, որ հայտարարել էր, որ ուներ ընդհանուր ապացույց իր ենթադրությունների հիման վրա, Ֆերման չթողեց իր ապացույցի մանրամասները։ Նա միայն թողեց այն հատուկ դեպքի՝ n = 4-ի ապացույցները։
Քանի որ հատուկ դեպքը՝ n = 4-ը ապացուցված էր, մնացել էր ապացուցել այն դեպքը, երբ n-ը պարզ թիվ է։ Հաջորդ երկու դարերի ընթացքում (1637–1839) վարկածը ապացուցվեց միայն 3, 5 և 7 պարզ թվերի համար։
Իսկ եթե ունենք հավասարում, որտեղ դրանցից ոչ մեկը հավասար չէ զրոյի, ուրեմն այդ հավասարումը ունի լուծում։ Որպեսզի համեմատություն կատարենք, սկսում ենք նախնական բանաձևից։

Այս թեորեմի վերջնական ապացուցումը ստացվել է 1994թ. Էնդրյու Ուալսի կողմից (Andrew Wiles ) և համարվում է XX դարում մաթեմատիկական գիտության աամենամեծ հաջողություններից մեկը:
Վերջում հետաքրքիր է լսել հետևյալ հանճարեղ երկխոսությունը՝ ՄԱԹԵՄԱՏԻԿՈՍԸ ԵՎ ՍԱՏԱՆԱՆ ։
Մաթեմատիկայի օլիմպիադայի դպրոցական փուլի երկրաչափական խնդիրները և նրանց լուծումները 2020թ.
7-րդ դասարան
4․C կետը AB հատվածի միջնակետն է, իսկ D կետը՝ BC հատվածի միջնակետը։ AC և CD հատվածների միջնակետերի հեռավորությունը 12 սմ է։ Գտնել AB հատվածի երկարությունը։
Լուծում.
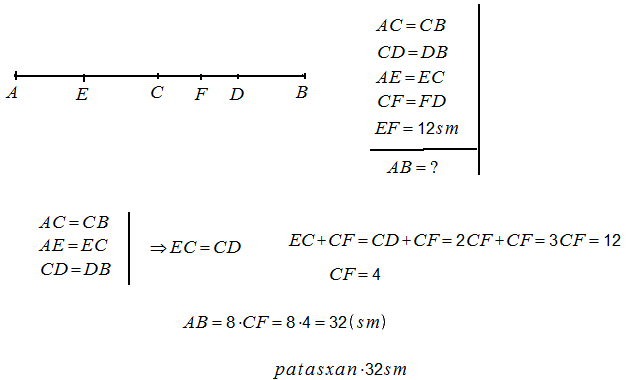
5․ AOC անկյան կից BOC անկյան ներքին տիրույթում տարված է OD ճառագայթը այնպես, որ COD անկյունը 420 է։ Գտնել AOC և BOD անկյունների կիսորդներով կազմված անկյունը։
Լուծում.
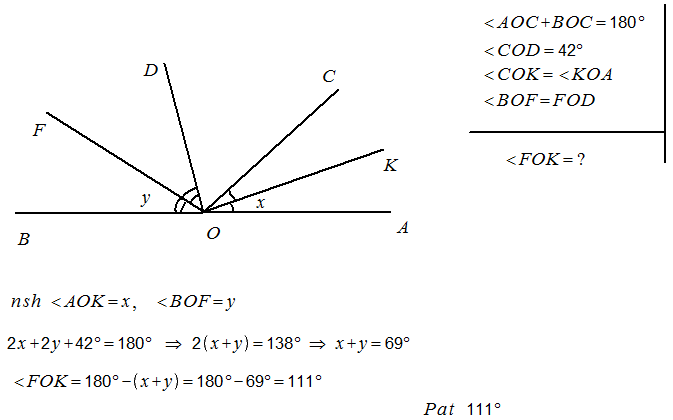
8-րդ դասարան
- ABC եռանկյան BM միջնագիծը 2 անգամ փոքր է AB կողմից և նրա հետ կազմում է 40 աստիճանի անկյուն: Գտնել ABC անկյան աստիճանային չափը:
Լուծում.
- Սեղանի անկյունագծերը փոխուղղահայաց են: Նրանցից մեկը 6 է, իսկ մյուսը հիմքի հետ կազմում է 30 աստիճանի անկյուն: Գտնել սեղանի միջին գծի երկարությունը:
Լուծում.
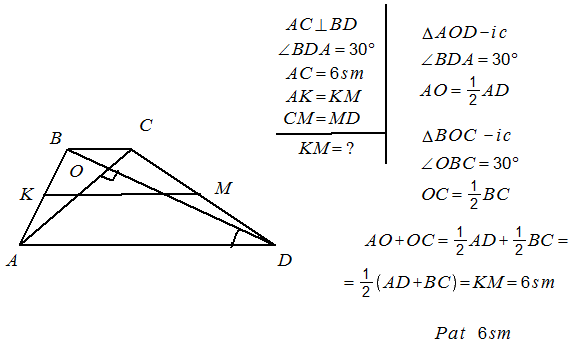
- ABC եռանկյան A ներքին անկյան և C արտաքին անկյան կիսորդները հատվում են M կետում: Գտնել BMC անկյան աստիճանային չափը, եթե անկյուն A-ն 40 աստիճան է:
Լուծում.
9-րդ դասարան
- 𝐴𝐵𝐶 եռանկյան 𝐴𝐵 կողմի վրա վերցված է 𝐸 կետ։ Գտնել 𝐴𝐵𝐶 անկյան աստիճանային չափը, եթե հայտնի է, որ 𝐴𝐸 = 𝐵𝐶 = 2, 𝐸𝐶 = √3, 𝐴𝐶 = √7:
Լուծում.
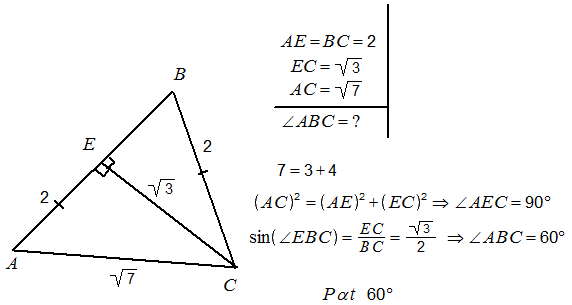
- Գտնել 𝑦 = 2𝑥 − 1, 𝑦 = −0,5𝑥 + 4 ուղիղներով և 𝑂𝑋 առանցքով սահմանափակված
պատկերի մակերեսը։
Լուծում.
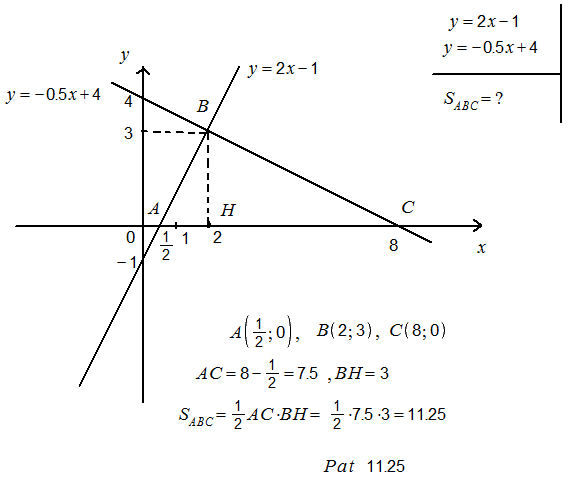
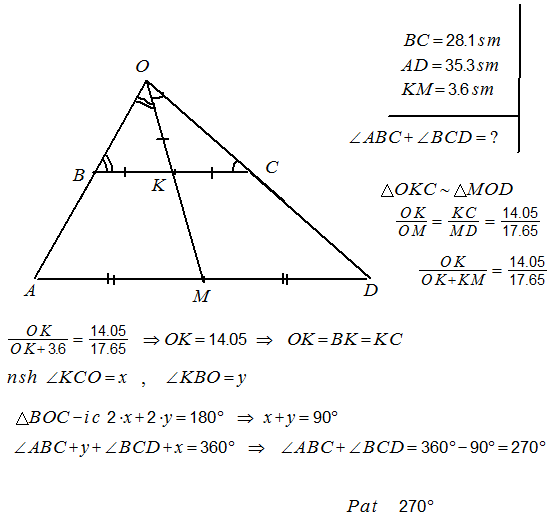
- Սեղանի հիմքերի միջնակետերը միացնող հատվածի երկարությունը 3,6 սմ է, իսկ հիմքերը՝ 35,3 սմ և 28,1 սմ։ Գտնել սեղանի փոքր հիմքին առընթեր անկյունների գումարը։
Լուծում.
Դաս 3









1

2.

3.

4.
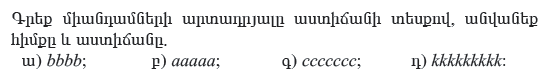
5.

6.

7.

Էլեկտրականության Փոխարեն Ֆոտոններ․ ԱԲ-Ի Զարգացման Նոր Հեռանկարները
Հետազոտողներն Արհեստական բանականության զարգացման ոլորտում նոր առաջընթաց են գրանցել․ հաշվարկները կատարելու համար նրանք էլեկտրականության փոխարեն լույս են օգտագործել։ Այս մեթոդը զգալիորեն բարելավվում է նյարդային ցանցերի մեքենայական ուսուցման արագությունն ու արդյունավետությունը։ Սա այն է ինչին ձգտում են գիտնականները՝ ստեղծել ԱԲ-ի մի ձև, որը կվերարտադրի մարդու ուղեղի կողմից կատարվող գործառույթները: ԱԲ-ն կսովորի ինքնուրույն և առաջադրանքները կկատարի ինքն իրենով՝ առանց հսկողության։

Մեքենայական ուսուցման համար օգտագործվող ժամանակակից պրոցեսորները բարդ գործողությունների կատարման համար բավականին թույլ են։ Որքան խելացի ու ընդգրկուն են առաջադրանքները, այնքան բարդ են տվյալները և, հետևաբար, առաջանում է խնդիր՝ կապված պրոցեսորի հզորության հետ։
Ջորջ Վաշինգտոն համալսարանի (ԱՄՆ) հետազոտողները պարզել են, որ նյարդային ցանցերում ֆոտոնների օգտագործումը, թույլ կտա հաղթահարել այդ սահմանափակումներն ու ստեղծել ավելի հզոր և էներգաարդյունավետ ԱԲ։
Նորարարական պրոցեսորի համար պոտենցիալ կոմերցիոն հավելվածները ներառում են 5G և 6G ցանցեր, ինչպես նաև՝ տվյալների մշակման կենտրոններ, որոնց հանձնարարված է իրականացնել տվյալների մեծ հոսքերի մշակում: Ըստ մշակողների, ֆոտոնային մասնագիտացված պրոցեսորները կարող են խնայել մեծ քանակությամբ էներգիա, կրճատել պատասխան ազդանշանի ժամանակն ու կրճատել տվյալների մշակման կենտրոնների շարժը:
Կատարված հետազոտության արդյունքները հրապարակվել են Applied Physics Reviews ամսագրում։
Ֆիզիկոսները Ապացուցել Են Էլեկտրոնների Քվանտային Տելեպորտացիայի Հնարավորությունը
Մարդկանց և մակրոաշխարհի այլ օբյեկտների հեռատեղափոխությունը (տելեպորտացիան) դեռևս շարունակվում է դասվել ֆանտաստիկայի ժանրին, սակայն քվանտային ֆիզիկայի ենթաատոմային համակարգում տեղեկատվության հեռատեղափոխությունը սովորական երևույթ է։ Անցած տարի գիտնականները հաստատել են, որ հնարավոր է միկրոչիպերում գտնվող և միմյանց հետ ֆիզիկապես կապ չունեցող ֆոտոնների միջև տեղեկատվության փոխանցումը։ Իսկ այժմ ապացուցել են, որ նույնը հնարավոր է նաև էլեկտրոնների համար։
Ռոչեստերի և Պերդյուի համալսարանների (ԱՄՆ) ֆիզիկոսները ուսումնասիրել են նոր մեթոդներ՝ առանձնացված էլեկտրոնների միջև քվանտային փոխազդեցության ստեղծման համար։ Նրանց ուսումնասիրությունների արդյունքում հնարավոր կլինի քվանտային համակարգիչների զարգացման նոր տեխնոլոգիաների ստեղծումը, ինչն էլ իր հերթին հնարավորություն կտա բժշկության, գիտության և տեխնիկայի թռիչքաձև զարգացմանը։
Քվանտային խճճվածությունը (entanglement) մի մասնիկի հատկությունների ազդեցությունն է մյուսի հատկությունների վրա՝ անգամ այն դեպքում, երբ վերջիններս գտնվում են միմյանցից մեծ հեռավորության վրա։ Այս ֆենոմենը մեծ դեր ունի հաշվիչ տեխնիկայում տեղեկատվության փոխանցման համար։ Այն դեպքում, երբ դասական համակարգիչը բաղկացած է միլիոնավոր տրանզիստորներից, քվանտայինում տեղեկատվությունը կոդավորում են քյուբիթներում (քվանտային բիթեր), որոնք կարող են միաժամանակ ընդունել զրոյի և մեկի արժեք։ Քյուբիթերի միաժամանակ մի քանի վիճակ ունենալու կարողությունն է դրված քվանտային համակարգիչների հիմքում։
Անցյալում գիտնականները քվանտային տելեպորտացիան ստացել էին էլեկտրամագնիսական ֆոտոնների օգնությամբ՝ ստեղծելով միմյանցից որոշակի հեռավորության վրա գատնվող քվանտային խճճված զույգեր։ Սակայն կա տեղեկատվության փոխանցման ևս մեկ հավանական տարբերակ՝ քյուբիթեր հիմնված առանձնացված էլեկտրոնների վրա։
Ինչպես նշում է հետազոտողներից Ջոն Նիկոլը՝ առանձնացված էլեկտրոնները հեշտորեն փոխազդում են մինյանց հետ, իսկ առանձնացված էլեկտրոններից կազմված քյուբիթերը կարելի է ստանալ կիսահաղորդիչներում։
Գիտնականները իրենց հետազոտություններում օգտագործել են Հայզենբերգի պատկերացումը։
Այս սկզբունքի կիրառմամբ՝ որոշել են էլեկտրոնների խճճված զույգերը և հեռատեղափոխել նրանց մագնիսական մոմենտները։ Նրանց հաջողվել է փոխազդեցություն առաջացնել այնպիսի էլեկտրոնների միջև, որոնք երբևէ չեն ունեցել ազդեցություն միմյանց վրա։ Քվանտային հեռատեղափոխության հնարավոր լինելը քվանտային համակարգիչների զարգացման նոր ուղի է և այն հնարավոր կլինի իրականացնել անգամ առանց ֆոտոնների կիրառման։
Փորձի արդյունքները նոր ճանապարհ են բացում քվանտային հեռատեղափոխության ուսումնասիրման համար։
Հետազոտությունը հրապարակվել է Nature Communications ամսագրում։
Երբ Գիտական Ֆանտաստիկան Դառնում Է Իրականություն․ Էներգիա՝ Տիեզերքից
Երկրագնդի ուղեծրում էներգիա առաջացնող պլատֆորմի ստեղծման գաղափարը առաջին անգամ շրջանառության մեջ է դրվել ինժեներ Փիթեր Գլասերի կողմից, սակայն այն տարածում գտավ միայն որոշ գիտնականների շրջանում, և ֆինանսական ու տեխնոլոգիական դժվարությունների պատճառով դարձավ գիտական ֆանտաստիկայի նյութ։

Այժմ, շնորհիվ զարգացած տեխնոլոգիաների ու ահռելի ներդրումների, գիտական ֆանտաստիկան հնարավորություն ունի տեսանելի ապագայում իրականություն դառնալու։
Չինաստանը պատրաստվում է վերականգնվող էներգետիկայի ոլորտում հեղափոխություն կատարել: Չինական տիեզերական տեխնոլոգիաների ակադեմիան աշխատանքներ է տանում ուղեծրային կայան ստեղծելու համար, որն արևային էներգիան կուտակելու է տիեզերքում և ապա փոխանցելու է Երկիր:

Նախատեսվող կայանը կտեղակայվի Երկրից 36000 կմ հեռավորության վրա։ Շնորհիվ նախատեսված շարժման ուղեծրի, այն մշտապես կունենա ուղիղ հասանելիություն դեպի արևը, միաժամանակ բացառելով մթնոլորտի ներգործությունը, այս եղանակով էներգիայի արտադրության արդյունավետությունը կավելանա մոտ 6 անգամ՝ համեմատած Երկրի արևային էլեկտրակայանների հետ:
Ըստ նախագծողների, արևային էլեկտրակայանը մարդկության համար ճանապարհ կբացի դեպի «մաքուր էներգիայի անսպառ աղբյուր»: Երկիր փոխանցելու համար էլեկտրական էներգիան նախ կվերածվի միկրոալիքային կամ լազերային ճառագայթների, այնուհետև կփոխանցվի Երկր:

Նշենք, որ առաջարկվող տեխնոլոգիայում տիեզերական էլեկտրակայանից կուտակված էներգիան դեպի Երկիր տեղափոխվոլու է միկրոալիքային ճառագայթներով, որը նշանակում է այս ճառագայքենրի անընդհատ ներգործություն Երկրի վրա։ Այս տեսանկյունից անհրաժետ է գնահատել միկրոալիքների երկարաժամկետ ազդեցությունը Երկրի մթնոլորտի և էկոլոգիայի վրա։
Նախքան ծրագրի վերջնական իրականացումը, դեռևս, գոյություն ունեն տեխնիկական բազմաթիվ խնդիրներ, որոնց լուծման ուղիները դեռ միանշանակ չեն, ինչպես, օրինակ՝ էլեկտրակայանի զանգվածը, որը նախատեսվում է լինել 1000 տոննա, ինչը գերազանցում է Միջազգային տիեզերակայանի զանգվածից 2,5 անգամ (վերջինս 400 տոննա է):

Հետազոտողները ուսումնասիրում են 3D տպիչների և անդրոիդների օգնությամբ տիեզերքում էլեկտրակայան կառուցման հնարավորությունը, ինչը հնարավորություն կտա խուսափել Երկրից ծանր սարքավորումների տեղափոխելուց:
Առաջին փորձարարական տիեզերական էլեկտրակայանի շինարարությունն արդեն սկսվել է Չունցին քաղաքում: Սկզբնական շրջանում չինացի գտնականները պլանավորում են կառուցել և գործարկել փոքր և միջին արևային էլեկտրակայաններ ստրատոսֆերայում (մթնոլորտի վերին շերտ՝ վերնոլորտ), որտեղ կարտադրվի էլեկտրաէներգիա 2021-ից 2025 թվականներին: Հաջորդ քայլը, ենթադրաբար, արեգակնային կայանի կառուցումն է, որի հզորությունը մինչև 2030 թվականը կլինի մոտ մեկ մեգավատ։
ԴԱՍ 2.





1.

2.Գրի՛ր (d−b)⋅(d−b)⋅(d−b) արտադրյալը աստիճանի տեսքով:
3.

4.

5.
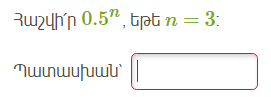
6.

7.

8.Գտիր քառակուսու մակերեսը, եթե դրա կողմը հավասար է՝ 1.2 մմ:
9.
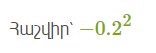
10.

11. Ներկայացրու՛ 44 թիվը աստիճանի և պարզ թվի արտադրյալի տեսքով:
12.
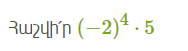
13.

ԴԱՍ 1
Թվային և հանրահաշվական արտահայտություններ






ԱՌԱՋԱԴՐԱՆՔՆԵՐ
1.Գտիր −9.1−8 արտահայտության արժեքը:
Պատասխան՝
2. Կարդա՛ 2.9+(−5) արտահայտությունը և գտի՛ր դրա արժեքը:
Տրված արտահայտության մեջ գրված է թվերի արտադրյալ թվերի քանորդ թվերի գումար թվերի տարբերություն :
Պատասխան՝
3. Հաշվիր (4+ 6
) ÷ 433 արտահայտության արժեքը:
Պատասխան՝
4. Առավել ռացիոնալ եղանակով գտիր 42.4⋅− 2.4⋅
արտահայտության արժեքը:
Պատասխան՝
5. Հաշվիր հանրահաշվական արտահայտության արժեքը, եթե a= 5, b=3
Պատասխան՝
6. արտահայտությունը x փոփոխականի ո՞ր արժեքի դեպքում իմաստ չունի:
Ընտրի՛ր ճիշտ տարբերակը:
- x=5 արժեքի դեպքում
- x=9 արժեքի դեպքում
- x=0 արժեքի դեպքում
- x=−5 արժեքի դեպքում
7. Արդյո՞ք իմաստ ունի հետևյալ կոտորակը՝
Պատասխան՝ կոտորակը իմաստ ունի կոտորակը իմաստ չունի
Հաշվի՛ր տրված կոտորակի արժեքը, եթե այն իմաստ ունի:
Եթե կոտորակն իմաստ չունի, ապա որպես պատասխան գրի՛ր «ոչ»:
Պատասխան՝
8. 9⋅11+12:3−2 արտահայտության մեջ փակագծերը տեղադրի՛ր այնպես, որ արտահայտության արժեքը լինի ամենափոքրը:
Բազմապատկման նշանի փոխարեն օգտագործիր * նշանը:
Պատասխան՝
«Սեբաստացու օրեր» կրթահամալիրի տոն ուսումնական նախագիծ
Կրթահամալիրի տարեդարձի պատվին ստեղծում ենք մեր անվանական <<էտյուդներ մաթեմատիկոսների մասին>> ժողովածուն:
Մասնակիցներ՝ 9-րդ, 10-րդ , 11-րդ դասարանցիներ
Ժամկետը՝ Նոյեմբերի 9-13
Օգտագործվող միջոցները՝թվային գործիք
Նպատակը՝ Սովորողներին մտածել սովորեցնել, դրդել ուսումնասիրելու այլ գրականություններ, ծանոթանալ մաթեմատիկոսների կյանքին, նշել իրենց կարծիքով ամենահանճարեղ մաթեմատիկոսին: Այս ամենը զարգացնելու, ոգևորելու, սովորեցնելու շահեր են հետապնդում:
Ընթացքը՝ Նախապես սովորողներին եմ ներկայացնում մեր անելիքները: Բոլոր դասարաններից յուրաքանչյուր սովորող պետք է այս ժամանակահատվածում պատրաստի մեկ նյութ իրենց սիրած մաթեմատիկոսի մասին: Նպատակահարմար է, որ նյութը կազմի ինքնուրույն՝ չօգտվելով վիկիպեդիա համակարգից կամ ընտանիքի անդամների օգնությամբ, բացի այդ հետաքրքիր լինի ու ոչ պարզունակ: Ուղարկում են սովորողները ինձ նյութերը և ըստ իրենց այդ մաթեմատիկոսի լավագույն թեորեմը, կամ օրենքը, ես հավաքագրում եմ դրանք մի ֆայլում, սովորողի անունը նշում նյութի դիմաց : Վերջում դրանք կհրապարկվեն իմ բլոգում, եթե ընթացքը հաջող լինի, կարելի է մտածել գրադարանի մի փոքր անկյունում ևս տեղ հատկացնելու մասին:





