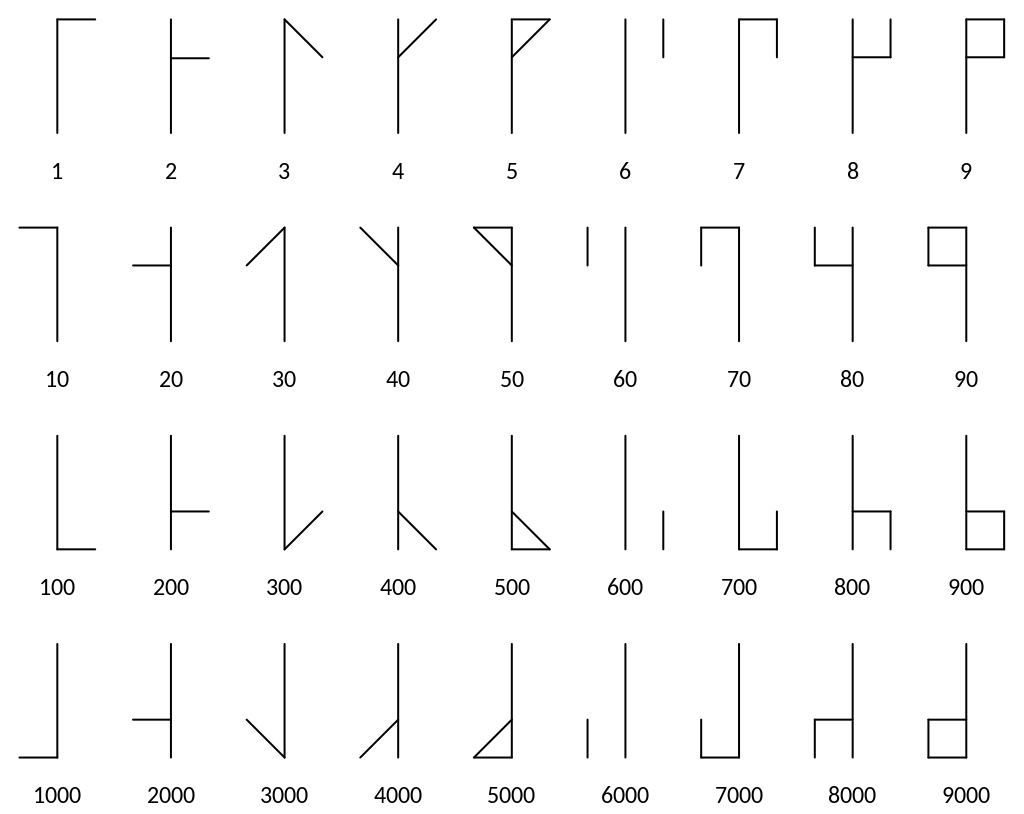

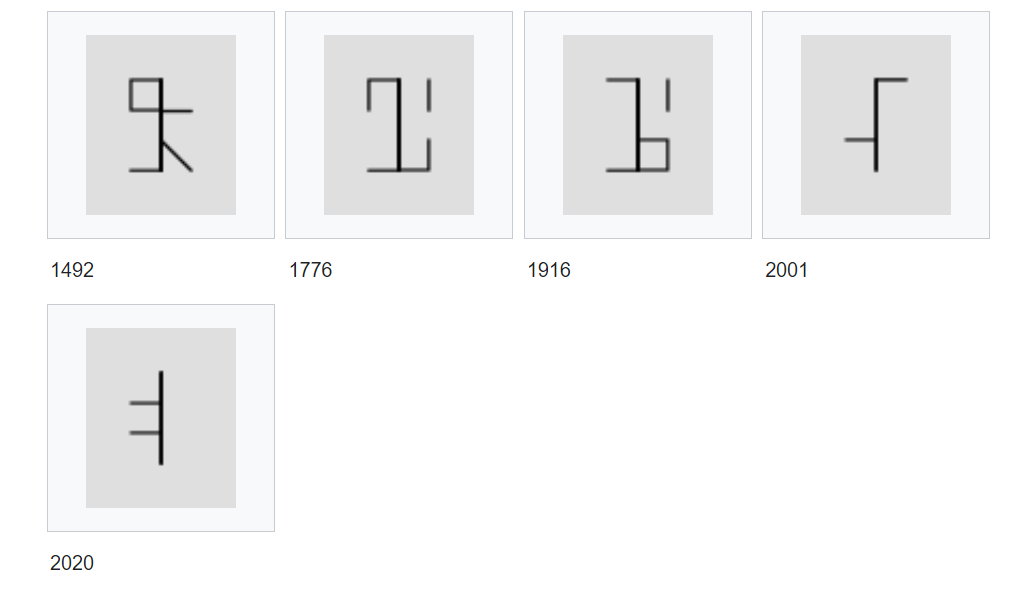
Ի՞նչ օրինաչափություն կա այս թվային համակարգի մեջ։



Ի՞նչ օրինաչափություն կա այս թվային համակարգի մեջ։
5 միտք
Պոեմը կարդում է Սուրեն Քոչարյանը։
8-րդ դասարան
1.1-ից մինչև 1000 ամեն բնական թվի համար գրատախտակին գրեցին իր բոլոր բաժանարարները (որոշակի թվեր գրատախտակին կգրվեն մեկից ավել անգամ): Այնուհետև հաշվեցին գրատախտակին գրված բոլոր թվերի գումարը։ Պարզել թե ստացված թիվը մեկ միլիոնից մե՞ծ է․ թե՞ փոքր։
Լուծում. Հաշվենք, թե յուրաքանչյուր բնական թիվ քանի՞ անգամ կգրվի գրատախտակին։ 1- ը կգրվի 1000 անգամ, քանի որ բոլոր թվերի համար էլ այն բաժանարար է։ 2-ը կգրվի 500 անգամ, քանի որ 1-ից 1000 միջակայքում կա 500 հատ զույգ թիվ։ 3-ը կգրվի 333 անգամ, 4-ը 250 և այսպես շարունակ, 999-ը կգրվի մեկ անգամ և 1000-ը կգրվի մեկ անգամ։ Նկատենք, որ 1-երի գումարը հավասար է 1000, 2-ների գումարը հավասար է 1000, 3-ների գումարը փոքր է 1000-ից (հավասար է 999) և այսպես մինչև 1000-ը։ Ուստի բոլոր գրված թվերի գումարը կլինի փոքր 1000 × 1000 = 1000000: Հետևաբար գրատախտակին գրված բոլոր թվերի գումարը փոքր է մեկ միլիոնից:
3. Գրատախտակին գրված 1, 2, 3, 4, ․․․, n բնական թվերը ներկված են սպիտակ: Յուրաքանչյուր քայլի թույլատրվում է գրատախտակին գրված թվերից ընտրել a <b< c <d չորս թվեր այնպես, որ b- a= c- b= d-c և նրանց գույները փոխել (սպիտակը՝ սև, իսկ սևը՝ սպիտակ): n –ի ո՞ր արժեքների դեպքում է հնարավոր այնպես անել, որ որոշակի քանակությամբ քայլեր անց գրատախտակին գրված բոլոր թվերը լինեն սև գույնի:
Լուծում. Սկզբում կա 0 քանակությամբ սև թիվ։ Առաջին քայլից հետո սև թվերի քանակը կդառնա 4 հատ։ Եվս մեկ քայլ անց սև թվերի քանակը կարող է դառնալ 0,2,4,6 կամ 8: Պարզ է, որ ցանկացած քանակությամբ քայլերից հետո սև թվերի քանակը զույգ է։ Քանի որ վերջում ցանկանում ենք ունենալ n հատ սև թիվ, ուստի 𝑛 = 2𝑘: Այժմ նկատենք, որ 𝑎, 𝑏, 𝑐, 𝑑 թվերից կամ բոլորը զույգ են, կամ բոլորը կենտ են, կամ էլ երկու հատը զույգ են և երկու հատը կենտ են։ Ամեն դեպքում նրանց մեջ կա զույգ քանակությամբ (0,2 կամ 4 հատ) զույգ թիվ։ Սկզբում կա 0 հատ սև թիվ, իսկ վերջում պետք է լինի 𝑘 հատ սև թիվ։ Քանի որ ամեն քայլի փոխվում է զույգ քանակությամբ զույգ թիվ, ուստի պետք է 𝑘-ն նույնպես զույգ լինի։ Այսպիսով 𝑛 = 2𝑘 = 4𝑠: Այժմ ցույց տանք, որ 4-ի բաժանվող n -երի համար հնարավոր է բոլոր թվերը սարքել սև։ Իսկապես, սկզբում սև սարքենք 1,2,3,4 թվերը, հաջորդ քայլին 5,6,7,8, այնուհետև 9,10,11,12 և այսպես շարունակ մինչև 4𝑠 − 3,4𝑠 − 2,4𝑠 − 1, 4𝑠:


Ան-Նասիր Սալահ ադ-Դին Յուսուֆ իբն Այյուբյան (արաբ․՝ صلاح الدين يوسف بن أيوب (Ṣalāḥ ad-Dīn Yūsuf ibn Ayyūb),քրդ.՝ سەلاحەدینی ئەییووبی (Selahedînê Eyûbî), հայտնի է նաև որպես Սալահ ադ-Դին կամ Սալադին ( 1138, Թիքրիթ, Իրաք — մարտի 4, 1193, Դամասկոս, Սելջուկյան սուլթանություն), Եգիպտոսի և Սիրիայի առաջին սուլթան և Այյուբյան դինաստիայի հիմնադիր։ Քրդական ծագմամբ սուննի մուսուլման Սալադինը ղեկավարել է Լևանտում խաչակրաց պետությունների դեմ ռազմական արշավանքները։ Իր իշխանության գագաթնակետին նրա սուլթանությունն ընդգրկել է Եգիպտոսը, Սիրիան, Ջեզիրեն (Վերին Միջագետք), Հիջազը, Եմենը և Հյուսիսային Աֆրիկայի այլ շրջաններ։

Սալադինի խնդիրը: 12 մետաղադրամից մեկը կեղծ է: Երեք
կշռումով գտե՛ք կեղծ մետաղադրամը և պարզել ծա՞նր է, թե՞
թեթև իսկականից:
Նոյեմբեր ամիսը լիարժեք աշխատեցինք ֆիզիկական միջավայրում: Ինչպես որ նախատեսել էինք նոյեմբերին 6-րդ , 9-րդ, 10-րդ և 11-րդ, 12-րդ դասարանցիների հետ իրականացրեցինք նախատեսված բոլոր դասընթացները և նախագծերը:
Նոյեմբեր ամսում մասնակցել եմ մաթեմատիկայի ֆլեշմոբի հոկտեմբեր ամսվա խնդիրների քննարկմանը և լուծմանը:
Այս ամիս մասնակցել եմ մաթեմատիկա դասավանդողների հավաքին,որը Գևորգ Հակոբյանի հետ կայացել է նոյեմբերի 1, 8, 15, 22, 29, :
Իրականացրել եմ նաև Սեբաստացու օրեր. կրթահամալիրի տոն-2021 նախագիծը։
Ելնելով Ուսումնական պարապմունքի կազմակերպման կարգից, հոկտեմբեր ամսում ուսումնասիրեցինք.
9-դասարան հանրահաշիվ
9-րդ դասրան երկրաչափություն
թեմաները:
10-րդ, 11-րդ , 12-րդ դասարանների հետ ընդհանուր առմամբ նույնպես աշխատեցինք լիարժեք:
6-րդ դասարանցիների հետ անցանք հետևյալ թեմաները՝
Շատ հետաքրքիր և օգտակար նյութ, աշակերտների համար:
«Մխիթար Սեբաստացի» կրթահամալիր
(Մխիթար Սեբաստացի) կրթահամալիր Ավագ դպրոց
<<Մխիթար Սեբաստացի>> կրթահամալիր