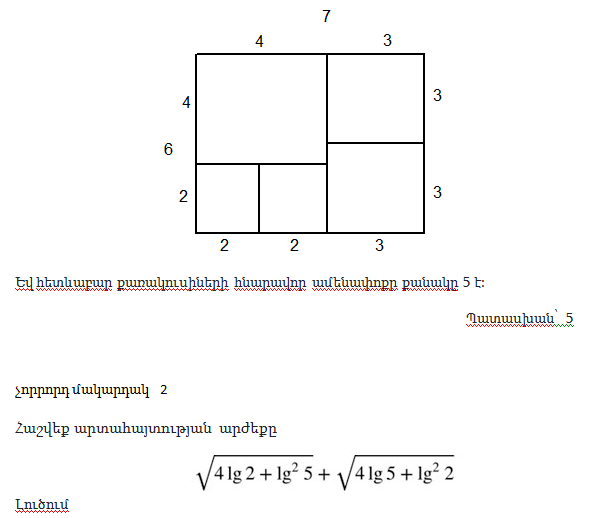Рубрика: ՖԼԵՇՄՈԲ

Նոյեմբերի ֆլեշմոբ մաթեմատիկայից  խնդիրներին կարող ենք ծանոթանալ նշված հղումով:

Հոկտեմբերի ֆլեշմոբի խնդիրների լուծումներին կարող ենք ծանոթանալ նշված հղումով:

Հոկտեմբերի ֆլեշմոբի իմ մասնակցությունը ֆլեշմոբի կայացմանը, ֆլեշմոբի երրորդ մակարդակի խնդիրների կազմելու և լուծումների տարբերակ տալու տեսքով էր:

Ստորևէ ներկայացնում եմ հոկտեմբերի ֆլեշմոբի որոշ խնդիրների լուծման իմ տարբերակը:

չորրորդ մակարդակ  4

4.Արկղում կան կարմիր, կանաչ, կապույտ և դեղին 100 գնդակներ: Առանց նայելու՝ ամենաքիչը քանի՞ գնդակ է պետք հանել արկղից, որ գոնե տասը գնդակներ լինեն միևնույն գույնի:

Լուծում. Մենք  պետք է քննարկենք, այսպես ասած, վատագույն դեպքը: Քննարկենք նախավերջին քայլը: Այսինքն, եթե գնդակները  հանել ենք և ստացել ենք 9-կարմիր,  9-կանաչ, 9- կապույտ,  9-դեղին  գնդակներ: Հաջորդ հանված  գնդակը  արդեն կդարձնի 10 գնդակ միևնույն գույնի: Գումարելով այս թվերը  կստանանք  խնդրի  պատասխանը՝   9+9+9+9+1 = 37:

                                                                                                                  Պատասխան՝   37

չորրորդ մակարդակ  7

7.Առավելագույնը քանի՞ հատ 2×2×1 չափանի աղյուս է հնարավոր տեղադրել 3 կողով խորանարդի մեջ:

Լուծում. Քանի որ խորանարդը  ունի  կենտրոնական  սիմետրիկություն, հետևաբար  հետևաբար  կապ  չունի  թե  որ  նիստն  որպես  հիմք  կվերցնենք: Աղյուսները կարող ենք դասավորել հետևյալ կերպ: Խորանարդի հիմքին իրար վրա կդնենք երեք աղյուս, որից հետո կմնա ուղղահայաց երկու աղյուսի տեղ: Դրանք էլ տեղադրելով կստանանք առավելագույնը 5 աղյուս:

                                                                                                                        Պատասխան՝  5

չորրորդ մակարդակ  7

10. Փոքր քառակուսու գագաթները գտնվում են մեծ քառակուսու կողմերի վրա: Գտեք փոքր քառակուսու մակերեսը, եթե CH= 5, BF=3:

Լուծում.

Հոկտեմբերի ֆլեշմոբը մաթեմատիկայից խնդիրներին կարող ենք ծանոթանալ նշված հղումով:

Հոկտեմբերի ֆլեշմոբի իմ մասնակցությունը ֆլեշմոբի կայացմանը, ֆլեշմոբի երրորդ մակարդակի խնդիրների կազմելու և լուծումների տարբերակ տալու տեսքով էր:

Ստորևէ ներկայացնում եմ հոկտեմբերի ֆլեշմոբի երրորդ մակարդակի խնդիրների իմ տարբերակը:

1.Տուփի մեջ կա 7 քարտ: 1-ից 7 թվերը գրված են այդ քարտերի վրա, ընդ որում, յուրաքանչյուր քարտի վրա գրված է մեկ թիվ: Առաջին իմաստունը տուփից վերցնում է 3 քարտ, իսկ երկրորդ իմաստունը` 2 քարտ: Առաջին իմաստունն ասում է երկրորդին. «Ես գիտեմ, որ քո քարտերի վրա գրված թվերի գումարը զույգ է»: Գտեք առաջին իմաստունի վերցրած քարտերի վրա գրված թվերի գումարը:

2.Հայկն ունի 9 տուփ, յուրաքանչյուրում՝ 2 կոնֆետ, իսկ նրա քույր Աննան՝ 8 տուփ, յուրաքանչյուրում՝ 5 կոնֆետ: Եթե Հայկը իր տուփերից մի քանիսը տա Աննային, իսկ Աննան էլ իր տուփերից մի քանիսը, բայց ոչ ստացածները, տա Հայկին, նրանք կունենան հավասար քանակությամբ կոնֆետներ: Ամենաքիչը քանի՞ տուփ նրանք պետք է տան միմյանց:

3.Թիվը կոչվում է պոլինդրոմ, եթե նրա թվանշանները հակառակ կարգով գրելիս, թիվը չի փոխվում: Գտեք ամենամեծ վեցանիշ պոլինդրոմ և ամենափոքր հնգանիշ պոլինդրոմ թվերի տարբերությունը:

4.Զբոսաշրջիկը մի քաղաքից մյուսը հասավ 3 օրում: Առաջին օրը նա անցավ ամբողջ ճանապարհի 1/5-ը և էլի 60 կմ, երկրորդ օրը՝ ամբողջ ճանապարհի 1/4-ը և էլի 20 կմ, իսկ երրորդ օրը՝ ամբողջ ճանապարհի 23/80-ը և մնացած 25 կմ-ը: Գտեք քաղաքների հեռավորությունը:

5.Ծաղկավաճառի մոտ մնացել է 24 սպիտակ, 42 կարմիր և 36 դեղին վարդ: Առավելագույնը քանի՞ միանման ծաղկեփունջ կարող է նա պատրաստել, եթե ուզում է օգտագործել բոլոր ծաղիկները:

6.ԳՈՐ X ԻՍ=7632 բազմապատկման օրինակում օգտագործված են մեկից մինչև ինը բոլոր թվանշանները: Ո՞ր թվանշանին է փոխարինում «Ո» տառը:Мой ответ7.Տղան 1 մ կող ունեցող խորանարդը բաժանեց 1 դմ կողով խորանարդների, դրանք միմյանց վրա դնելով՝ կառուցեց աշտարակ: Գտեք այդ աշտարակի բարձրությունը:

8.Մաթեմատիկայի խնդրագրքի բնագրում կար մի վարժություն, որտեղ պահանջվում էր տրված թիվը բազմապատկել 3-ով և ստացված արդյունքից հանել 4: Էջադրողը սխալվեց. բազմապատկման նշանի փոխարեն դրեց բաժանման նշան, իսկ հանման նշանի փոխարեն՝ գումարման նշան: Բայց այնուամենայնիվ, վերջնական արդյունքը չփոխվեց: Ի՞նչ վարժություն էր խնդրագրքում:

9. Անգլիացի մաթեմատիկոս Օգյուստ դե Մորգանը ասում էր, որ նա եղել է 𝑋 տարեկան 𝑋^2 թվականին: Հայտնի է, որ նա մահացել է 1899 թ.-ին: Ե՞րբ է նա ծնվել:

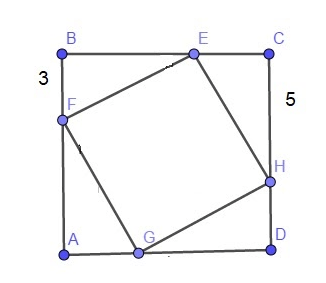
10.Նայելով նկարին՝ գտեք α+β-ն։

Սեպտեմբերի ֆլեշմոբին առաջադրված խնդիրների լուծումներին կարող ենք ծանոթանալ նշված հղումով:

Սեպտեմբերի ֆլեշմոբի իմ մասնակցությունը ֆլեշմոբի կայացմանը, լուծումների տարբերակ տալու տեսքով էր:

Ստորևէ ներկայացնում եմ սեպտեմբերի ֆլեշմոբի որոշ խնդիրների լուծման իմ տարբերակը:

Սեպտեմբերի ֆլեշմոբը մաթեմատիկայից խնդիրներին կարող ենք ծանոթանալ նշված հղումով:

Օգոստոսի ֆլեշմոբին առաջադրված խնդիրների լուծումներին կարող ենք ծանոթանալ նշված հղումով:

Օգոստոսի ֆլեշմոբը մաթեմատիկայից կարող ենք ծանոթանալ նշված հղումով:

Հուլիսյան ֆլեշմոբ մաթեմատիկայից նույնպես անցավ շատ հետաքրքիր: Հուլիսյան ֆլեշմոբի իմ մասնակցությունը ֆլեշմոբի կայացմանը, խնդիրների տարբերակ առաջարկելու, և լուծումների տարբերակ տալու տեսքով էր:

Ստորևէ ներկայացնում եմ հունիսյան ֆլեշմոբի որոշ խնդիրների լուծման իմ տարբերակը:

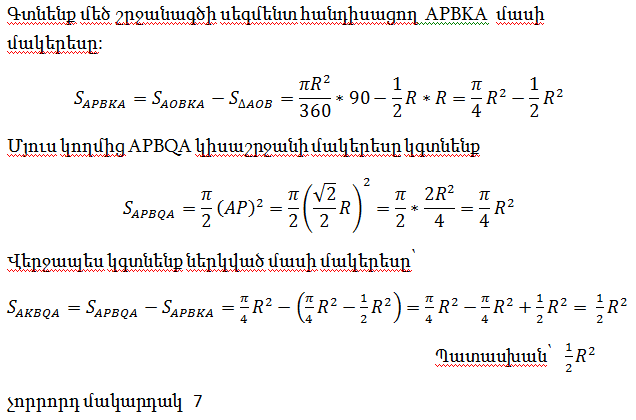
Հուլիսյան ֆլեշմոբ մաթեմատիկայից նույնպես անցավ շատ հետաքրքիր: Հուլիսյան ֆլեշմոբի իմ մասնակցությունը ֆլեշմոբի կայացմանը, խնդիրների տարբերակ առաջարկելու, և լուծումների տարբերակ տալու տեսքով էր:

Ստորևէ ներկայացնում եմ հունիսյան ֆլեշմոբի չորրորդ մակարդակի խնդիրները:

1. Հնգանիշ թիվն անվանենք հետաքրքիր, եթե դրա բոլոր թվանշանները տարբեր են, և a=b+c+d+e: Քանի՞ հետաքրքիր հնգանիշ թիվ գոյություն ունի:

2. Արկղում կան գնդակներ: Յուրաքանչյուր գնդակի վրա գրված է մեկական բնական թիվ: Բոլոր թվերը տարբեր են: Գնդակներից 30-ի վրա գրված է 6-ի բազմապատիկ թիվ, 20-ի վրա՝ 7-ի բազմապատիկ թիվ, իսկ 10-ի վրա՝ 42-ի բազմապատիկ թիվ: Առնվազն քանի՞ գնդակ կա արկղում:

3. Ռոբին Հուդը երեք անգամ նետահարում է, և բոլոր նետերը դիպչում են թիրախին (տես նկարը): Ընդամենը քանի՞ տարբերակ կա միավորների գումար վաստակելու։

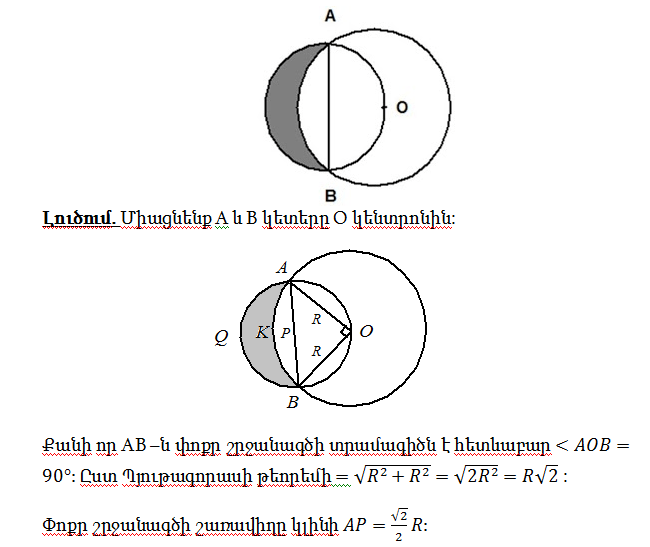
4. AB-ն նկարում պատկերված շրջանագծերից փոքրի տրամագիծն է, իսկ մեծի O կենտրոնը փոքր շրջանագծի վրա է: Մեծ շրջանագծի շառավիղը R է: Որքա՞ն է ներկված մասի մակերեսը:

5. Տրված է երկու թվաբանական պրոգրեսիա՝ 5,20,35,… և 35,61,87, … : Բնական թվերի քանի՞ թվաբանական պրոգրեսիա կա, որտեղ այդ երկու հաջորդականություններից յուրաքանչյուրը ենթահաջորդականություն է:

6. A վայրից դեպի B վայր դուրս եկավ բեռնատար մեքենան: Միաժամանակ B-ից A շարժվեց մարդատար մեքենան: Բեռնատարը 1 ժամ հետո հանդիպեց մարդատարին և ևս 1,5 ժամ հետո հասավ B վայր: Որքա՞ն ժամանակ ծախսեց մարդատար մեքենան B-ից A ճանապարհին:

7. Եթե երկնիշ թվին գումարենք նույն թվանշաններով կազմված թիվ՝ հակառակ դասավորությամբ, կստանանք լրիվ քառակուսի: Գտեք այս պայմանին բավարարող երկնիշ թվերի քանակը:

8. Պապիկը իր 33 թոռներին և ծոռներին բաժանեց 180 խաղալիք այնպես, որ յուրաքանչյուր ծոռ ստացավ մեկ խաղալիքով ավելի, քան յուրաքանչյուր թոռ: Քանի՞ թոռ և քանի՞ ծոռ ունի պապիկը, եթե հայտնի է, որ բոլոր ծոռները ստացան այնքան խաղալիք, որքան բոլոր թոռները:

9. Նարեկը գրեց բոլոր եռանիշ թվերը և յուրաքանչյուր թվի համար գտավ դրա թվանշանների արտադրյալը: Դրանից հետո տղան գտավ բոլոր ստացված արտադրյալների գումարը: Արդյունքում ի՞նչ թիվ ստացավ Նարեկը:

10. Օլիմպիադայի մասնակիցներից հինգը դարձան հաղթողներ՝ հավաքելով 15, 14 կամ 13 միավոր և համապատասխանաբար գրավելով առաջին, երկրորդ և երրորդ տեղերը: Քանի՞ մասնակից գրավեց երկրորդ տեղը, եթե հինգը միասին հավաքել են 69 միավոր:

Խնդիրները ընտրեց Թաթուլ Շահնազարյանը:

Հունիսյան ֆլեշմոբ մաթեմատիկայից նույնպես անցավ շատ հետաքրքիր: Հունիսին իմ մասնակցությունը ֆլեշմոբի կայացմանը, խնդիրների լուծումների տարբերակ առաջարկելու տեսքով է: Ստորևէ ներկայացնում եմ հունիսյան ֆլեշմոբի խնդիրների լուծման իմ տարբերակը: