Рубрика: 9 Հանրահաշիվ և մաթեմատիկական անալիզի տարրեր

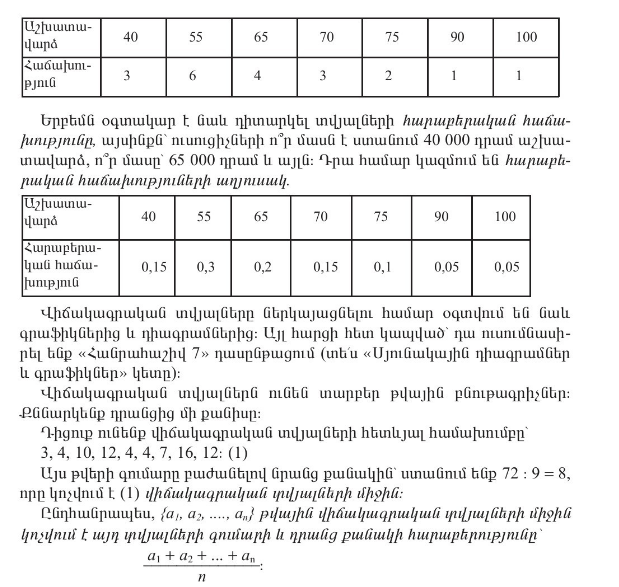
Սեպտեմբերի ֆլեշմոբ մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես երկրորդ մակարդակի

1. Գտե՛ք այն երկնիշ թվերի քանակը, որոնց միավորը մեծ կամ հավասար է տասնավորին։

2. Երկու հաջորդական կենտ թվերի արտադրյալը հավասար է 143: Գտե՛ք այդ թվերի գումարը:

4. Մայրիկը սեղանին թողել էր 9 կտոր շոկոլադ և յուրաքանչյուր 30 րոպեն մեկ երեխային թույլ էր տվել ուտել միայն մեկ կտոր։ Առաջին կտորն ուտելուց քանի՞ ժամ անց կվերջանան շոկոլադի կտորները, եթե երեխան լսի իր մայրիկին և միանգամից չուտի ամբողջ շոկոլադը:

5. Արամը կերավ ափսեում եղած ծիրանների 3/11 մասը, Արմանը կերավ մնացած ծիրանների 3/8 մասը, արդյունքում ափսեում մնաց 10 ծիրան։ Սկզբում քանի՞ հատ ծիրան կար ափսեում:

խնդիրները:

Հուլիսի ֆլեշմոբը մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես երկրորդ մակարդակի

1. Գտե’ք այն ամենափոքր թիվը, որը երկուսի, երեքի, չորսի բաժանելիս ստացվում է 1 մնացորդ, իսկ 5-ի բաժանվում է առանց մնացորդի:

2. Շոկոլադե սալիկը, տե՛ս նկարը, բաղկացած է երկու տարբեր գույնի շոկոլադներից, որոնցից յուրաքանյուրը 12 կտոր է: Տիգրանը ուզում է կտրել 2×2 սալիկ այնպես, որում երկու գույնի շոկոլադե կտորների քանակները լինեն իրար հավասար: Քանի՞ հնարավոր տարբերակ կա:

3. Շախմատի մրցաշարին մասնակցեց 7 մարդ: Մասնակիցներից յուրաքանչյուրը մնացածների հետ խաղաց մեկական պարտիա: Ընդամենը քանի՞ պարտիա անցկացվեց:

9. Պատկերը ներկիր այնպես, որ հարևան (ընդհանուր գիծ ունեցող) ցանկացած երկու մասեր լինեն տարբեր գույն, տե՛ս նկարը: Ամենաքիչը քանի՞ գույն կարող ես օգտագործել:

խնդիրները:

Հուլիսի ֆլեշմոբը մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես չորրորդ մակարդակի

4. Տրված է PQRS քառակուսին և PS կողմի M միջնակետը: Որքա՞ն է QMS եռանկյան և PQRS քառակուսու մակերեսների հարաբերությունը:

3. Շրջանագծի վրա նշված է 17 կետ: Նրանցից յուրաքանչյուրը միացված է մյուսների հետ, բացի իր անմիջական հարևաններից: Քանի՞ լար կստացվի:

1. 3 թվի 40 տոկոսը բազմապատկեցին 3 թվի 60 տոկոսով: Արդյունքում 3 թվի քանի՞ տոկոսը ստացվեց:

խնդիրները:

Հուլիսի ֆլեշմոբը մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես երրորդ մակարդակի

1. Եռանիշ թիվը 12 անգամ մեծ է իր թվանշանների գումարից: Գտե՛ք այդ թիվը:

2. Վերելակը 1-ին հարկից 6-րդ հարկ բարձրանում է 30 վայրկյանում: Քանի՞ վայրկյանում վերելակը կբարձրանա 1-ին հարկից 3-րդ հարկ (վերելակը շարժվում է հավասարաչափ):

3. Խաղի ժամանակ խաղադաշտում գտնվող մի թիմի ֆուտբոլիստների (11 հոգի) միջին տարիքը 22 տարեկան է: Երբ Ֆուտբոլիստներից մեկը դուրս եկավ խաղադաշտից, դաշտում մնացած 10 ֆուտբոլիստների միջին տարիքը դարձավ 21 տարեկան: Գտե՛ք խաղադաշտից դուրս եկած ֆուտբոլիստի տարիքը:

4. Մի ամսվա երեք կիրակի օրերն եղան զույգ թվեր: Շաբաթվա ի՞նչ օր էր այդ ամսվա 22-ը:

խնդիրները:

Հուլիսի ֆլեշմոբը մաթեմատիկայից խնդիրների քննարկումը, մասնավորապես

5. Գրապահարանի դարակի վրա որդը կրծել ու կարճագույն ճանապարհով անցել է Պուշկինի գրքի առաջին հատորի առաջին էջից մինչև կողքին գտնվող երկրորդ հատորի վերջին էջը: Յուրաքանչյուր հատորի էջերը միասին (հաստությամբ) 2սմ են, իսկ յուրաքանչյուր կազմի հաստությունը` 2մմ: Ի՞նչ հեռավորություն է անցել որդը:

8. Եթե երկնիշ թվի թվանշանների միջև զրո ավելացնենք, ստացված եռանիշ թիվը 9 անգամ մեծ կլինի սկզբնական թվից: Գտե՛ք այդ երկնիշ թիվը:

խնդիրների լուծում: